Aplicación de métodos estadísticos y predictivos (PCA, clustering y PLS-DA) sobre datos de vinos para obtener qué factores influyen más a la hora de elaborar un buen vino.
Miquel Marín Colomé & Álvaro Mazcuñán Herreros
1 – DESCRIPCIÓN DEL ESTUDIO Y DE LA BASE DE DATOS
1.1 – DESCRIPCIÓN DEL ESTUDIO
El siguiente trabajo está relacionado con una base de datos que trata sobre la variedad de vino tinto y vino blanco del ‘Vinho Verde’ portugués. La certificación del vino incluye pruebas fisico-químicas como por ejemplo, la determinación de la densidad, pH, cantidad de alcohol, etc. Con este proyecto, se quieren estudiar aquellas variables que influyan más a la hora de analizar la calidad de un vino, si es malo, bueno/regular o muy bueno.
1.2 – DESCRIPCIÓN DE LA BASE DE DATOS
La base de datos está formada por 12 variables y 4858 observaciones. La mayoría de las variables son componentes fisicoquímicos que se utilizan para la elaboración de los vinos. Dichas variables son las siguientes:
- Acidez fija
- Acidez volátil
- Ácido cítrico
- Azúcar residual
- Cloruros
- Dióxido de azufre libre
- Dióxido de azufre total
- Densidad
- pH
- Sulfatos
- Alcohol
Dichas variables enunciadas anteriormente son de tipo continuas. Aparte, se dispone de una variable ‘target’ o variable respuesta. Esta variable se corresponde con la calificación del vino y es de tipo discreta. Toma valores de 0 a 10.
2 – ANÁLISIS EXPLORATORIO INICIAL Y PREPROCESADO DE LOS DATOS
2.1 – DATOS FALTANTES
Primero, antes que nada, se investiga si existen valores faltantes en el fichero de datos. Se comprueba mediante la siguiente función y se observa que no hay ningún valor de dicho tipo.
## [1] 0
2.2 – TRANSFORMACIÓN DE VARIABLES
Una de las transformaciones que se han llevado a cabo ha sido la de la variable calidad del vino. Tal y como se puede observar, existen pocos valores de aquellas observaciones que toman como valoración 3, 4, 8 o 9.
## 3 4 5 6 7 8 9
## 20 163 1447 2178 870 175 5
Por ello, se ha decidido agrupar los valores que toma dicha variable en 3 grupos distintos:
- Grupo 1: Vinos con una valoración de 3 o 4. Se considerarán vinos ‘malos’
- Grupo 2: Vinos con una valoración entre 5 y 7. Se considerarán vinos ‘buenos’
- Grupo 3: Vinos con una valoración de 8 o 9. Se considerarán vinos ‘muy buenos’
2.3 – VARIABLES Y/O REGISTROS DESCARTADOS
Se ha hecho un estudio previo de la base de datos y se ha decidido no eliminar ninguna de las variables ya que, por una parte, todas son importantes y, por otra, al disponer solamente de 12, la eliminación de una de ellas podría provocar una pérdida de información a la hora de realizar el estudio.
2.4 – DISTRIBUCIÓN DE LAS VARIABLES
A continuación, se observarán cada una de las variables de las que se disponen, estudiando si existe, a priori, algún dato anómalo o extremo en ellas.
En el Anexo 8.3: Análisis distribución de las variables está todo explicado con mayor detalle, analizando si existe normalidad o asimetría en los datos, además del coeficiente de Kurtosis.
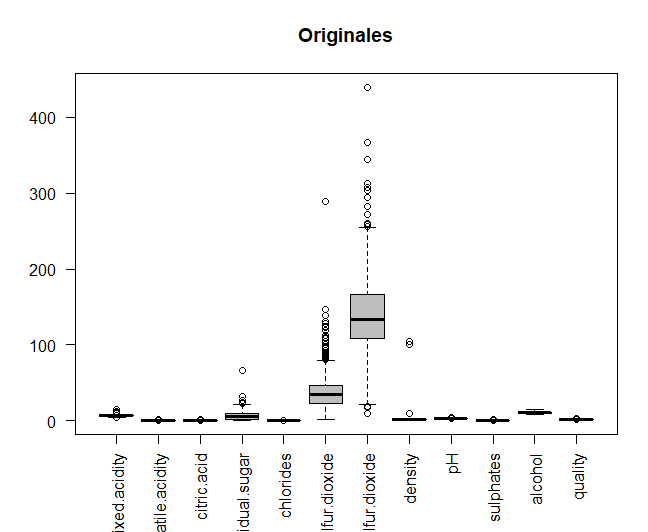
A priori, no se observan datos anómalos. Como único detalle, en la gráfica de densidad se puede observar que todas las observaciones toman valores alrededor de 1.
Estos son algunos de los valores de densidad de algunos vinos.
- Vino blanco seco: 0,9880-0,9930 g/mL.
- Vino tinto seco: 0,9910-0,9950 g/mL.
- Vino espumoso: 0,9890-1,0080 g/mL.
- Vino de licor (moscatel): 1,0500-1,0700 g/mL.
Por lo tanto, es un valor normal.
2.5 ESCALADO Y CENTRADO DE LOS DATOS
Una vez realizado un pequeño análisis exploratorio de los datos de este fichero, se pasa ya a la parte del preprocesado, parte importante antes de realizar los análisis convenientes.
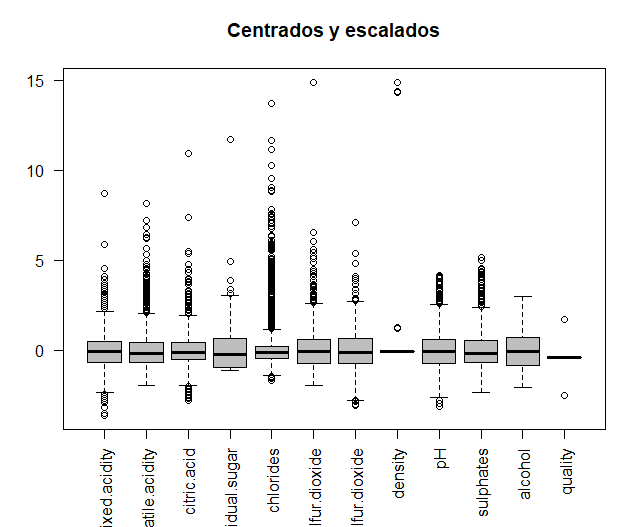
Se van a comparar los datos originales con los datos una vez centrados y escalados, para así poder observar si las variables están medidas en distintas magnitudes. Los datos son centrados y escalados.
A continuación, se imprime en una misma ventana los dos gráficos que permiten realizar la comparación, mediante la función par. Se puede observar como algunas de las variables se miden en distintas magnitudes, por ejemplo, los dos tipos de azufres. Por ello, para realizar los análisis posteriores, se utilizarán los datos centrados y escalados.
3. ANÁLISIS 1 – ANÁLISIS DE COMPONENTES PRINCIPALES (PCA)
Una vez ya realizado el análisis exploratorio y los datos han sido centrados y escalados, se puede pasar ya al primero de los tres análisis que se realizarán en este proyecto de la asignatura. El primero de ellos, como bien indica el título, es el análisis de componentes principales. La utilidad de este método es doble:
- Representar óptimamente en un espacio de dimensión pequeña, observaciones de un espacio general p-dimensional. Es el primer paso para identificar posibles variables ‘latentes’ o no observadas, que están generando la variabilidad de los datos.
- Permite transformar las variables originales, en general correlacionadas, en nuevas variables no correlacionadas, facilitando la interpretación de los datos.
3.1 OBJETIVOS
El objetivo al utilizar esta técnica será obtener las variables que más influyen en las dimensiones que más variabilidad explican. Utilizando este método se podrá obtener una visión más específica de como se comportan los datos que se están trabajando. Aparte, se realizará un pequeño estudio sobre algunos vinos que lleguen a tener datos extremos.
3.2 APLICACIÓN DEL MÉTODO / RESULTADOS NUMÉRICOS Y GRÁFICOS
SCREE-PLOT
Se pasa ya a la aplicación del método. Todo ello se realiza mediante la función PCA ya implementada en R. No se escalan los datos debido a que ya se ha realizado anteriormente.
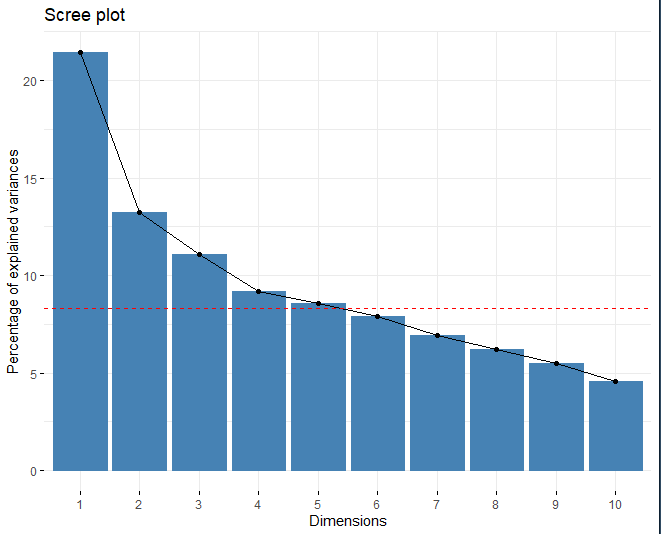
## eigenvalue variance.percent cumulative.variance.percent
## Dim.1 2.571633 21.434687 21.43469
## Dim.2 1.585109 13.211958 34.64665
## Dim.3 1.330253 11.087723 45.73437
## Dim.4 1.102265 9.187435 54.92180
## Dim.5 1.029659 8.582255 63.50406
Se aplica el método y se observa como el número de componentes principales ideal es de 5. Por una parte, mediante el scree plot, la línea roja corta en la quinta dimensión. Por otra parte, otra técnica para elegir el número de dimensiones adecuado es obtener aquellas componentes las cuáles tienen un valor propio mayor que 1. Pues bien, obteniendo una tabla con dicho valor propio correspondiente a cada una de las dimensiones se puede ver que, a partir de la quinta componente, el valor propio es mayor que 1.
SCORE-PLOT
A continuación, se obtiene un score plot con los scores de los vinos en cada una de las dimensiones que se han obtenido anteriormente. Dichos vinos están coloreados por su contribución en las componentes.
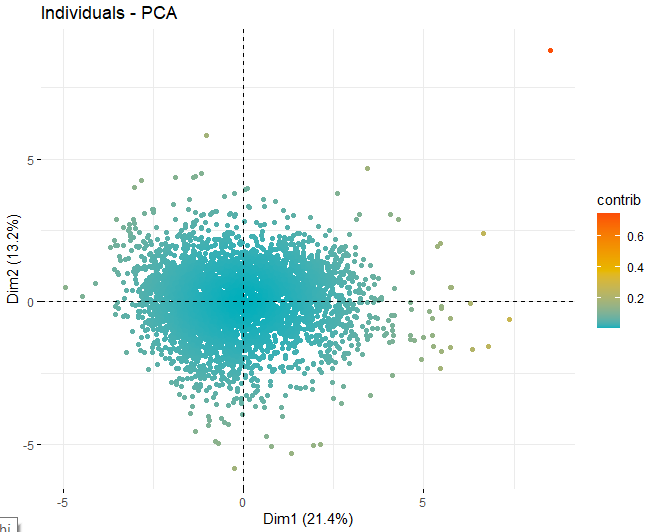
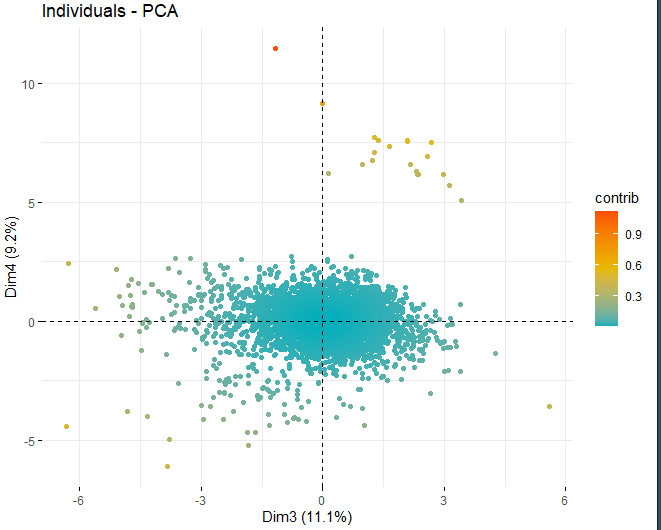
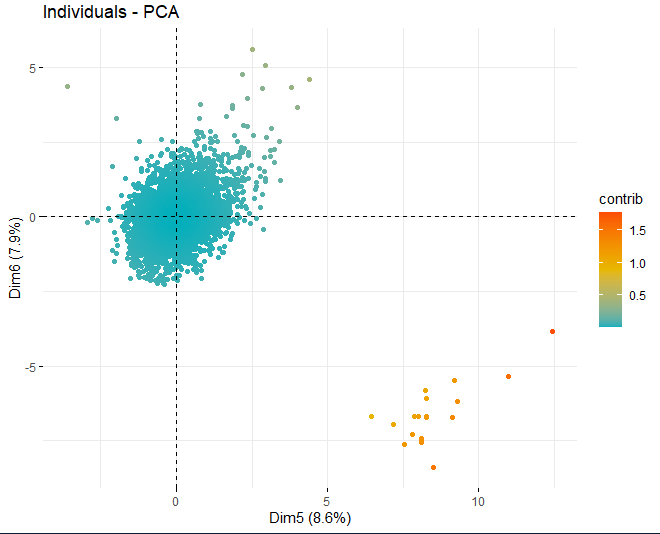
Se puede observar como existen algunos valores anómalos en las distintas componentes, aparte de unas pocas observaciones extremas que superan un score, en valor absoluto, mayor que 5 e incluso de 10. Para poder obtener más información de cuáles son dichas observaciones anómalas, se pasan a obtener los mismos scores plots de antes pero, en este caso, únicamente con las observaciones que superan un score, en valor absoluto, de 5.
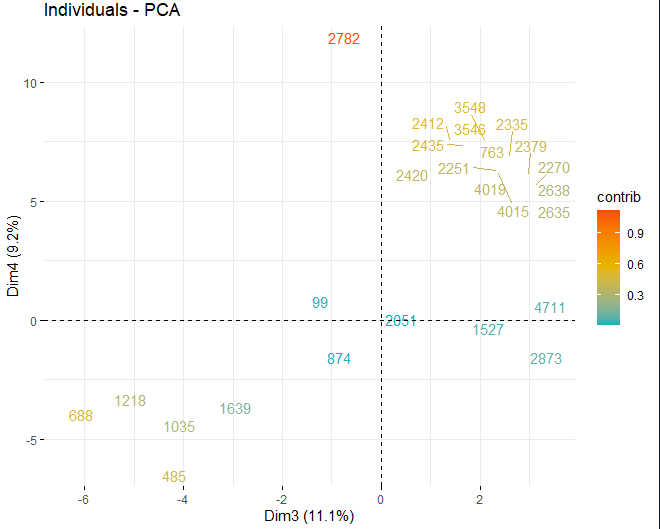
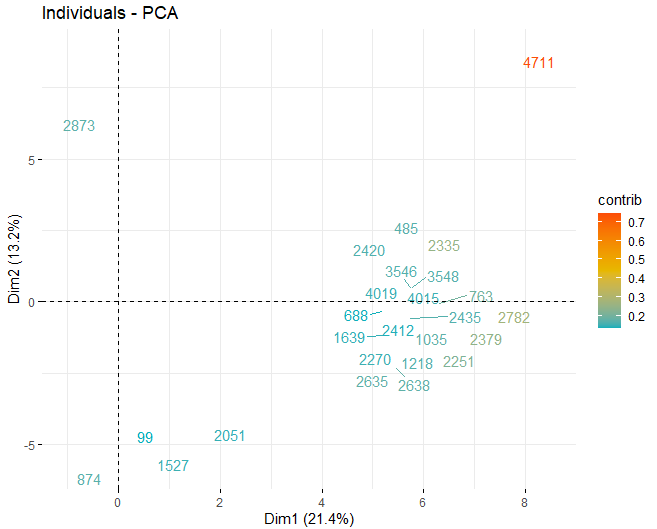
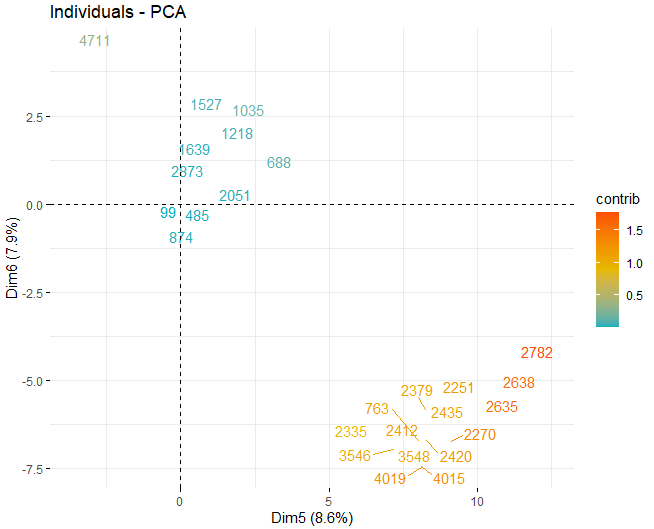
T2 HOTELLING
Algunas observaciones, concretamente los vinos 4711, 2782 o 2635, tienen unos valores muy extremos que, si se dejan en la base de datos, pueden llegar a distorsionar las conclusiones de unos futuros análisis. En concreto, se deberían eliminar aquellas observaciones que superasen un límite del 99% utilizando la T2 de Hotelling.
A continuación, se pueden observar algunos de los vinos que superan dicho límite.
Se observa que existen, en concreto, un total de 156 observaciones que superan el límite del 99%. 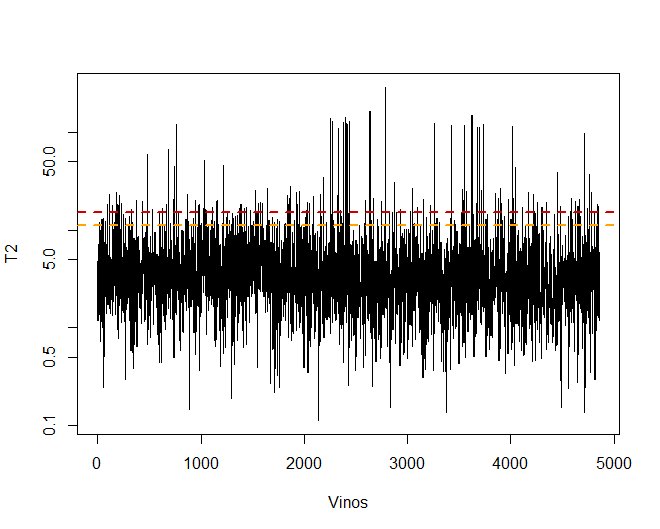
## [1] 156
Por ello, para realizar unos mejores análisis, se pasan a eliminar dichos vinos.
## [1] 4702 12
A continuación, se crea una variable auxiliar para guardar en ella la variable calidad, que se usará en el siguiente análisis para colorear.
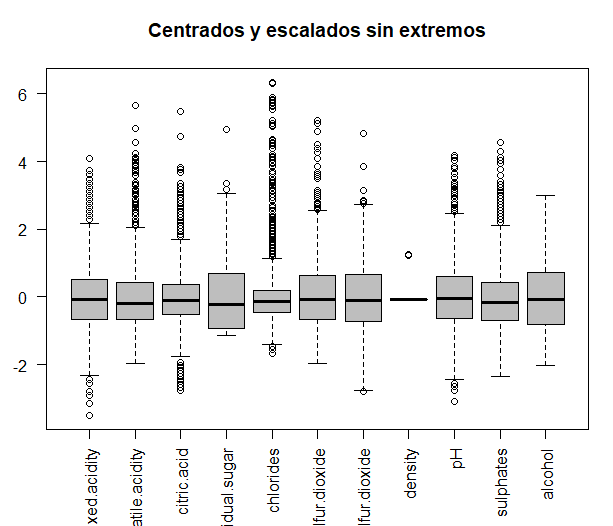
En este caso, observando el eje ‘y’ de los boxplots, eliminando los valores anteriores, ya no existen valores extremos. 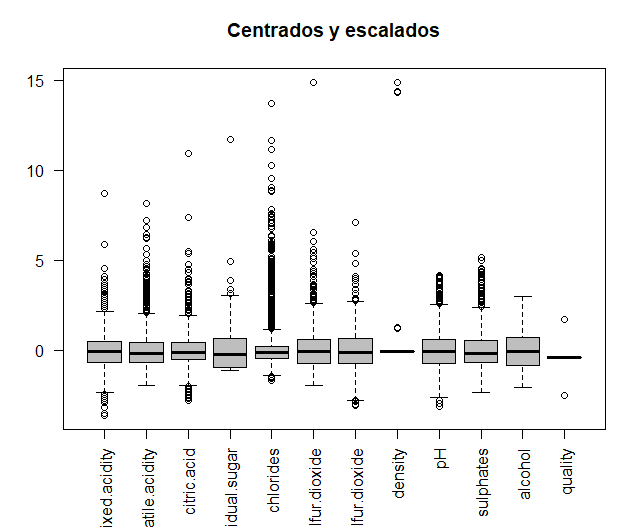
Ahora se tendría que volver a realizar el PCA, con las nuevas observaciones. En este caso, siguiendo los mismos criterios de antes (utilizando el scree plot y los valores propios de cada una de las dimensiones), se obtienen 3 componentes principales ya que éstas tienen un valor propio superior a 1.
## eigenvalue variance.percent cumulative.variance.percent
## Dim.1 2.3094622 26.079639 26.07964
## Dim.2 1.4442754 16.309503 42.38914
## Dim.3 1.0534806 11.896446 54.28559
## Dim.4 0.8526690 9.628779 63.91437
## Dim.5 0.8060166 9.101956 73.01632
LOADING-PLOT
Una vez obtenidas las dimensiones adecuadas, se pasan a obtener los loading plots de cada una de las dimensiones que se han obtenido anteriormente: 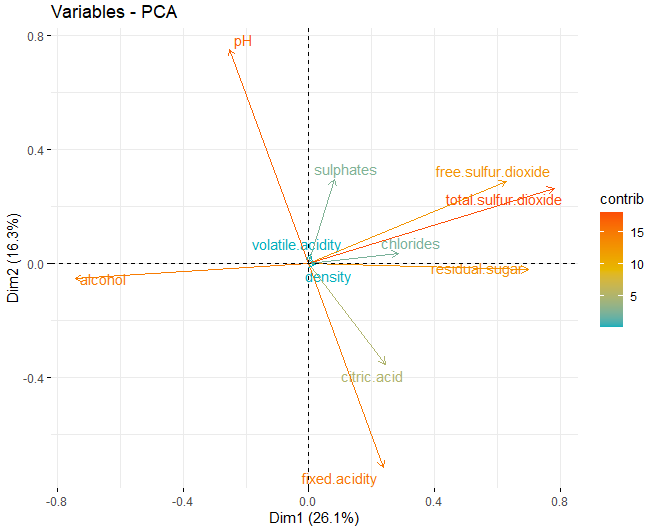
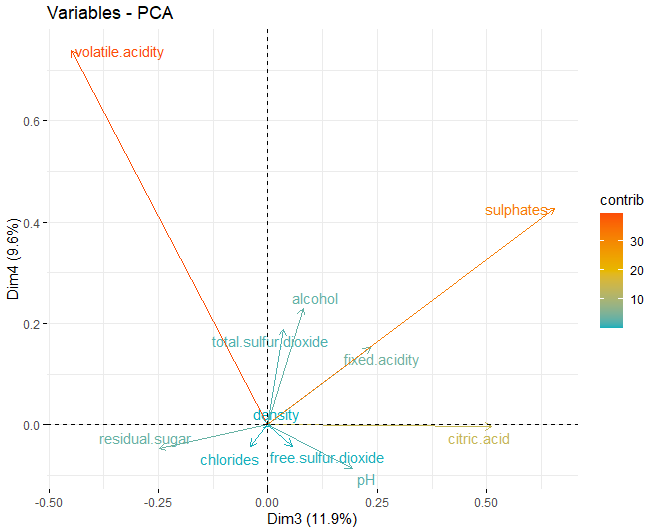
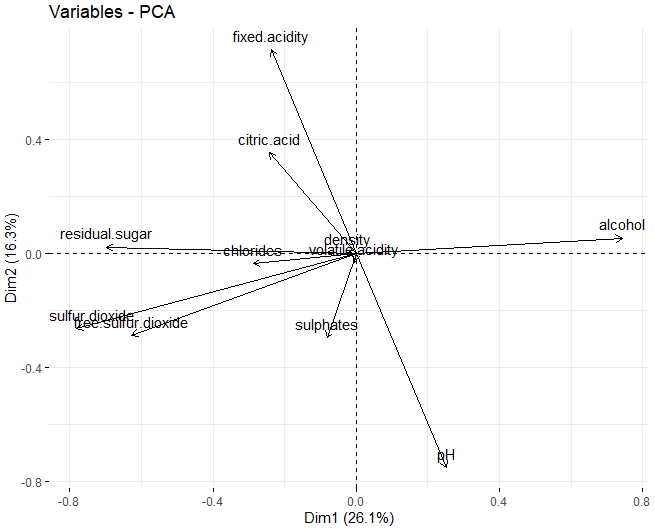
En este caso se puede observar que, en la primera dimensión, las variables que más influyen en dichas dimensiones son las componentes fisicoquímicas de alcohol, azúcar residual y los dos tipos de azufres, tanto el libre como el total. Por otra parte, en la segunda dimensión, las que más influyen son tanto el pH como la acidez fija.
3.3 DISCUSIÓN DE LOS RESULTADOS
En este primer objetivo se ha podido observar que es necesario la realización de más de un análisis PCA debido a las observaciones anómalas que pueden aparecer utilizando la T2 de Hotelling. Si dichos resultados se obviaron, probablemente los gráficos de scores y loadings no se interpretarían de la misma forma y se obtendrían resultados que no serían del todo reales.
Al margen de esto, mediante esta técnica, se ha podido obtener una visión más detallada de la base de datos que se está tratando, analizando las variables que más influyen en la creación de las dimensiones. Se ha podido observar que éstas son las del alcohol, azúcar residual y los dos tipos de azufres, el azufre libre y el total.
4. ANÁLISIS 2 – CLUSTERING
4.1 OBJETIVOS
El segundo análisis que se va a realizar en este proyecto va a ser el análisis de conglomerados o análisis clúster. El objetivo al aplicar esta técnica en concreto es obtener qué características son las más importantes a la hora de valorar la calidad de un vino utilizando técnicas de clustering jerárquico y algoritmos de partición. En términos de esta base de datos, el objetivo es obtener aquellas variables químicas que influyen en el valor que acaba tomando la variable respuesta, es decir, la variable quality.
Finalmente, se obtendrá un gráfico coloreado por calidad, para estudiar si realmente, los clusters que forma dichas variables, están bien separados o no.
4.2 APLICACIÓN DEL MÉTODO – RESULTADOS NUMÉRICOS
4.2.1 AGRUPACIÓN DE LOS DATOS – ESTADÍSTICO DE HOPKINS
Antes que nada, previo a la aplicación de dicho método, se tiene que estudiar si existe una agrupación en los datos que se están tratando. Esto se puede realizar mediante el coeficiente de Hopkins. Hay que recordar que cuanto más cerca esté ese coeficiente de 1, más agrupación existirá en los datos.
Se utiliza la función hopkins ya implementada en R pero, hay que tener cuidado, debido a que dicha función obtiene el coeficiente de una forma un tanto distinta. Calcula el estadístico al revés, es decir, el valor real de dicho coeficiente es de 1-H. Por lo tanto, en este caso 1-0.08 = 0.92. Por lo cual, se puede decir que existe una gran agrupación en los datos.
## $H
## [1] 0.1029338
4.2.2 HCPC – HIERARCHICAL CLUSTERING ON PRINCIPAL COMPONENTS
El HCPC es un algoritmo que agrupa individuos similares en clústers pero con una peculiaridad, está hecho para trabajar con los resultados de un método de componentes principales. Este algoritmo permite obtener un número de clusters óptimo mediante una técnica basada en la inercia. En el Anexo 8.1: Bibliografía se adjunta un link para más información acerca de este.
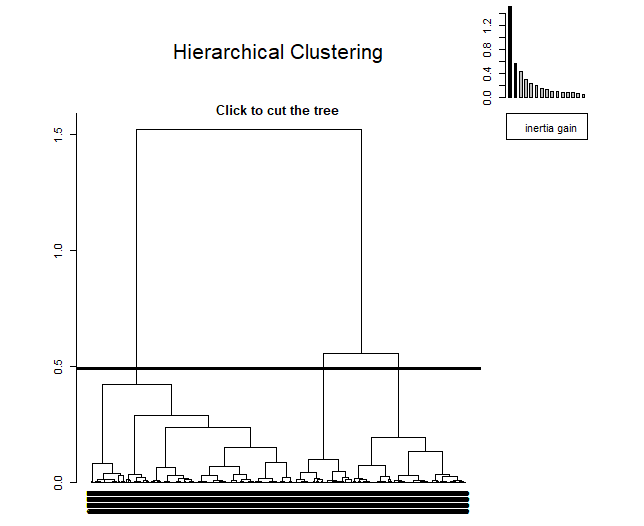
Al aplicarlo, se puede observar como, en la parte superior derecha, aparece un pequeño gráfico que indica la inercia en cada una de las dimensiones. El método decide coger tres clústers ya que, a partir de la tercera componente, la inercia se mantiene.
4.2.3 OBTENCIÓN MATRIZ DE DISTANCIAS
Una vez presentada una primera técnica para obtener el número óptimo de clústers, se pasa ya a la obtención de la matriz de distancias, utilizando la distancia euclídea ya que el objetivo es encontrar vinos con características similares para, posteriormente, estudiar si están clasificados como buenos o malos.
4.2.4 MÉTODO DE WARD
En primer lugar, se utilizará el método de Ward. El primero método ha encontrado el 3 como el número de clústers óptimo, por ello, se asignará k=3.
## grupos1
## 1 2 3
## 1743 2031 928
Se puede observar que, usando dicho método, los tres grupos formados parece que estén bien agrupados, sin datos aparentemente anómalos.
A continuación, se utilizarán los métodos del codo y Silhouette para validar el número de clústers óptimo para el método de Ward. 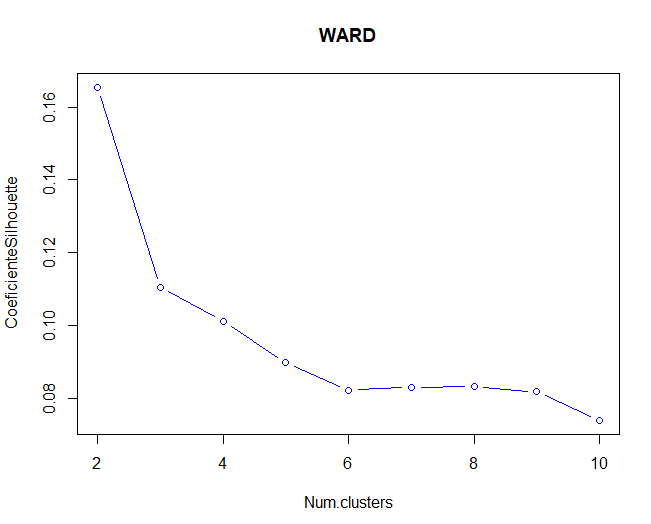
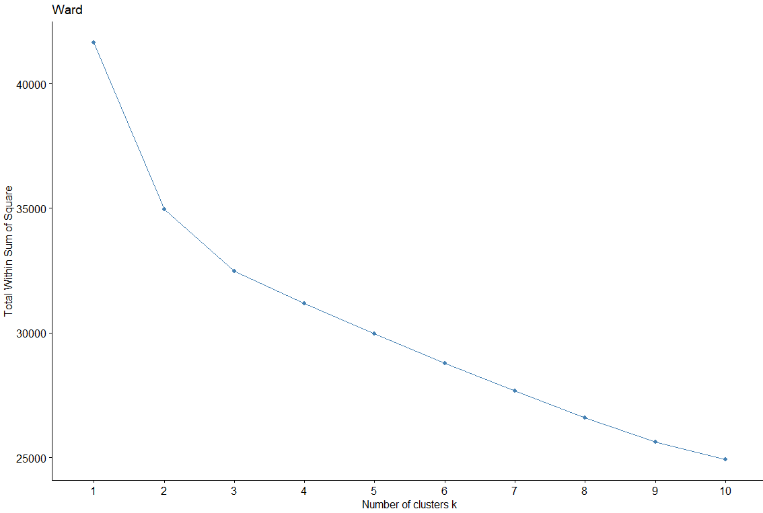
Se observa que, tanto para el método de Silhouette como para el método del codo (aunque no se ve tan claro), el número de clústers óptimo sería de 2 clústers. En este caso, utilizando dos clústers, aparecen más de 1000 observaciones en un grupo respecto de otro.
## grupos1b
## 1 2
## 1743 2959
4.2.5 K-MEANS
A continuación se estudia otro método, en este caso el método de Kmeans o Kmedias. Al igual que se ha hecho con el método de Ward, se asignará también en este caso k=3. Se observa también una buena agrupación de los datos utilizando tres clusters.
##
## 1 2 3
## 1683 1475 1544
Se pasa a obtener el método de clusters óptimo utilizando dicho método, también con el coeficiente de Silhouette y el método del codo. 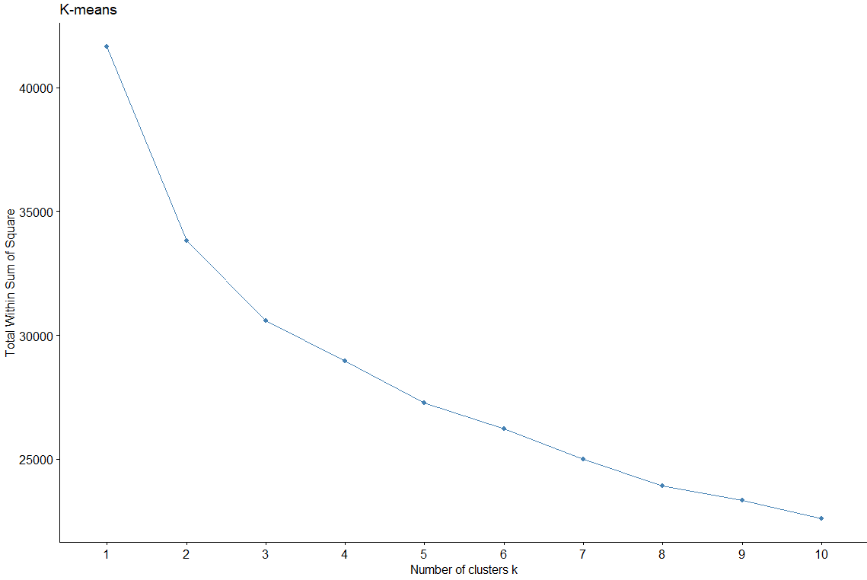
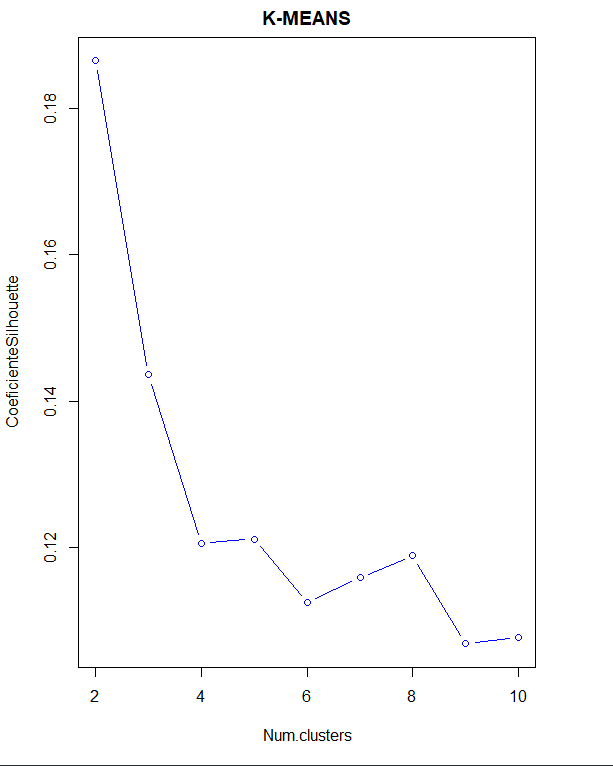
En este caso, en el método del codo, no se observa un codo tan definido. Sin embargo, estudiando el coeficiente de Silhouette, indica que el número de clusters es de 2 otra vez.
4.3 NÚMERO DE CLUSTERS ÓPTIMO – VALIDACIÓN DE LOS RESULTADOS
Una vez estudiados algunos métodos para obtener el número óptimo de clusters, se compararán dichos métodos utilizando el coeficiente de Silhouette para así poder validar los resultados.
Comparando las dos representaciones, se puede decir que el método de partición, el algoritmo k-means, funciona mejor que el método jerárquico de Ward debido a que el coeficiente de Silhouette es más elevado en ese caso. Además, en el caso del método de Ward, aparecen unas cuantas observaciones con valores negativos en el coeficiente que se está utilizando.
Por lo tanto, en el siguiente apartado, la interpretación de los resultados del clustering se van a estudiar utilizando el método del K-medias. Además, se utilizará dicho algoritmo con 3 clústers ya que, anteriormente, se ha podido observar que con ese valor K, los grupos estaban más balanceados, sin valores anómalos.
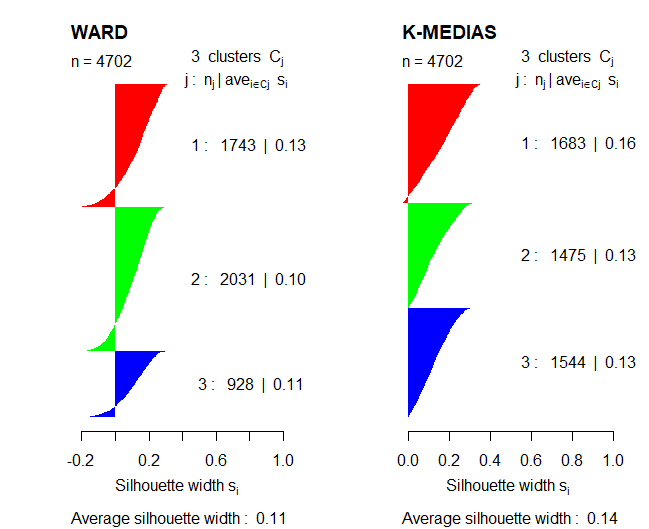
4.4 RESULTADOS GRÁFICOS
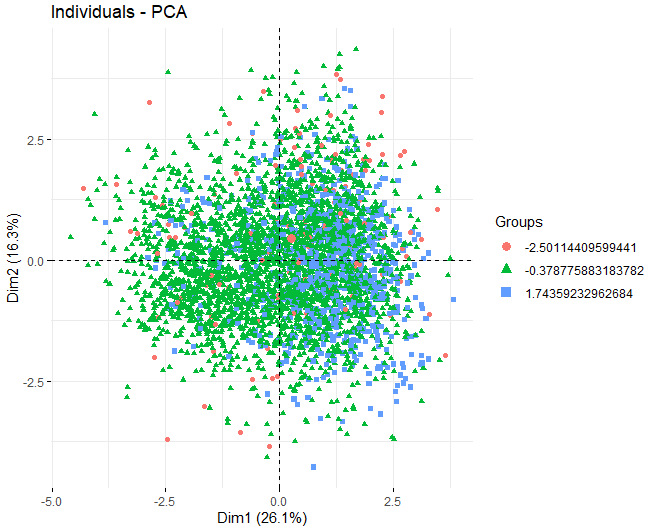
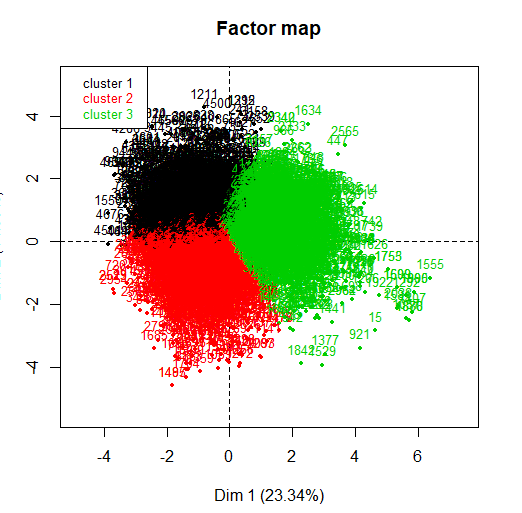
Una vez comentado que se va a utilizar el método del K-medias, se pasa a obtener un PCA para ver qué variables contribuyen más en la formación de los clústers. En este caso, se puede observar que, utilizando el algoritmo de k-means con 3 clústeres, los 3 grupos se separan muy bien, están balanceados.
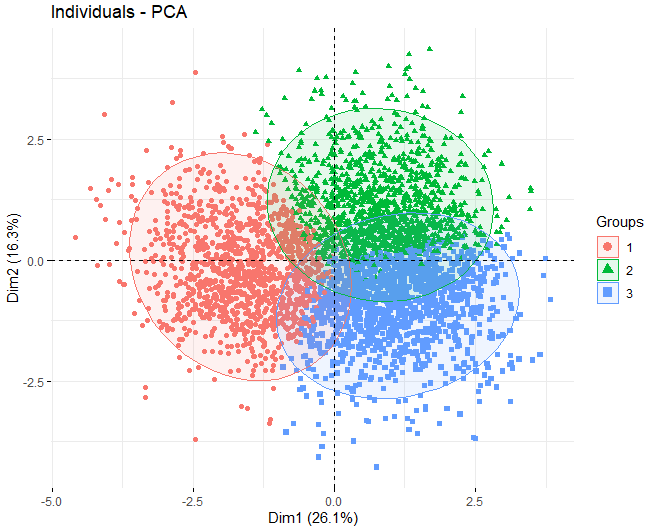
Se puede observar que, en las primeras dos dimensiones, las variables que más influyen en la creación de los clústers son el azúcar residual, el alcohol, y los dos tipos de azufres, tanto el azufre total como el azufre libre.
Finalmente, se pasa a mostrar un gráfico donde se representan cada uno de los vinos para observar si la variable calidad influye en la creación de los clústers. Se puede ver que los clústeres no están bien separados, la mayoría de los puntos se sobreponen con otros.
4.5 DISCUSIÓN DE LOS RESULTADOS
Mediante esta técnica se ha podido observar que la variable calidad no influye en la creación de los clústers. Esto podría ser debido a distintos factores que no se han tenido en cuenta en el análisis desde un principio. Puede que los clusters se lleguen a formar según otras variables como por ejemplo, la denominación de origen, el tipo de uva que se está usando para elaborar dichos vinos, etc.
5 ANÁLISIS 3 – PARTIAL LEAST SQUARES – DISCRIMINANT ANALYSIS (PLS-DA)
La técnica del PLS es una mezcla entre regresión múltiple y PCA. Hay que tener en cuenta que si existe multicolinealidad, la regresión puede que no se realice de forma correcta y no aparezcan los resultados deseados. Sin embargo, el PLS utiliza previamente el PCA para observar qué variables son las que más influyen en la creación de las variables que se están estudiando y cada una de las componentes es ortogonal a la siguiente que más influye y así sucesivamente. Por esa razón, gracias a que las componentes son linealmente independientes entre sí, la regresión se podrá llevar a cabo sin ningún problema.
Una de las variantes del PLS es el PLS-DA, que es la que se va a utilizar en este proyecto, la cual incluye la técnica del análisis discriminante. La diferencia, respecto a la técnica anterior, es que la variable respuesta es categórica. A partir de esta variable categórica se crearán tantas variables ‘Dummy’ como distintos valores pueda tomar esa variable respuesta.
5.1 OBJETIVOS
El objetivo al utilizar esta técnica es doble. Por una parte, estudiar posibles observaciones anómalas (a continuación, se explicará como poder tratarlas). Por otra parte, evaluar la capacidad predictiva de un modelo PLS-DA con la variable de la calidad del vino.
En la primera técnica que se ha utilizado, la del PCA, se ha podido observar que, utilizando la T2 de Hotelling, aparecían algunas observaciones que sobrepasaban el límite del 99%, considerándose observaciones anómalas y extremas las que se alejaban más de ese corte. En el PLS se realizará un procedimiento similar. Primeramente, se realizará un primer modelo PLS y, mediante la técnica de la T2 de Hotelling, se estudiarán posibles observaciones anómalas o extremas.
Se eliminarán aquellas observaciones que sobrepasen el límite del 99% mediante la T2 de Hotelling y entonces se volverá a crear un nuevo modelo PLS, para así obtener un modelo más fiable que otro con casos anómalos que puedan alterar sus características.
5.2 APLICACIÓN DEL MÉTODO
Se pasa ya a la aplicación del modelo. Primero hay que transformar la variable respuesta a factor ya que, aunque sea cualitativa, el programa no lo detecta de esa forma ya que toma valores numéricos.
Una vez aplicado, se puede observar como el modelo obtiene 3 como número ideal de componentes.
## PLS-DA
## 4858 samples x 11 variables and 1 response
## standard scaling of predictors and response(s)
## R2X(cum) R2Y(cum) Q2(cum) RMSEE pre ort pR2Y pQ2
## Total 0.405 0.116 0.113 0.337 3 0 0.05 0.05
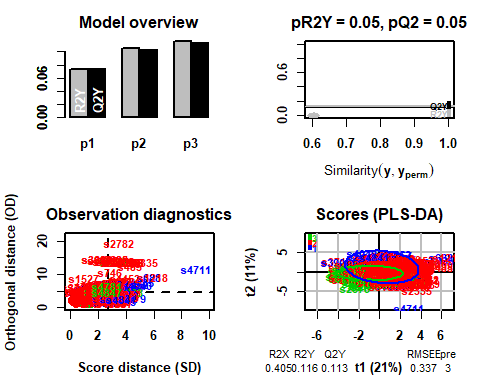
5.2.1 T2-HOTELLING
Lo primero que se debe realizar, una vez aplicado el modelo, es la validación de los datos, observar si existen observaciones anómalas o extremas que puedan influenciar en los resultados. Para ello, se realizará un gráfico de la T2 de Hotelling y de esta forma poder detectarlas.
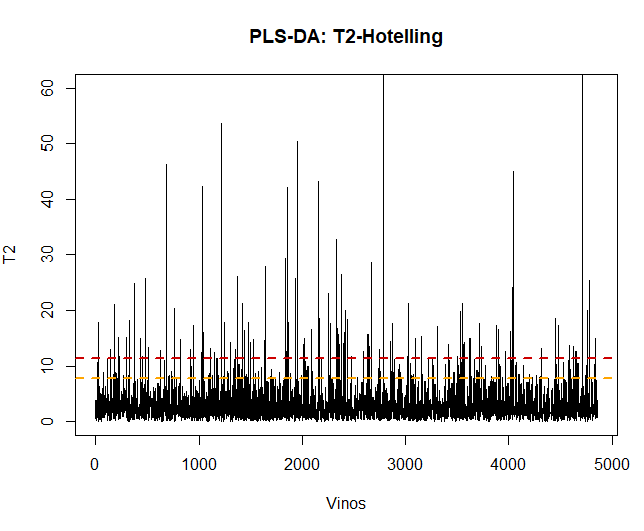
Utilizando dicha técnica, se puede ver que existen unas 100 observaciones anómalos. Dichos datos se eliminarán y se volverá a aplicar el modelo del PLS-DA.
## [1] 109
5.3 APLICACIÓN DEL MÉTODO SIN DATOS ANÓMALOS
En este caso se puede ver que, eliminando las observaciones anteriores, el modelo escoge en este caso 2
## PLS-DA
## 4749 samples x 11 variables and 1 response
## standard scaling of predictors and response(s)
## R2X(cum) R2Y(cum) Q2(cum) RMSEE pre ort pR2Y pQ2
## Total 0.31 0.104 0.101 0.337 2 0 0.05 0.05
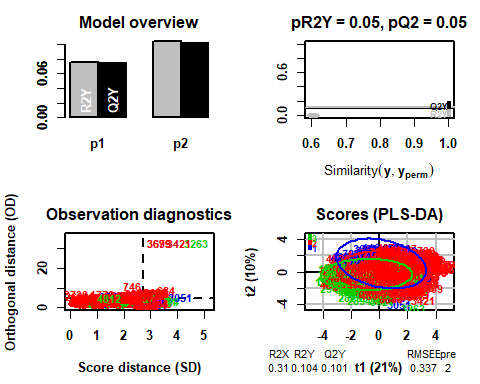
5.3.1 T2-HOTELLING
Si se visualiza ahora el gráfico de T2 de Hotelling, ya no existen datos anómalos que pueden llegar a influenciar en el modelo.
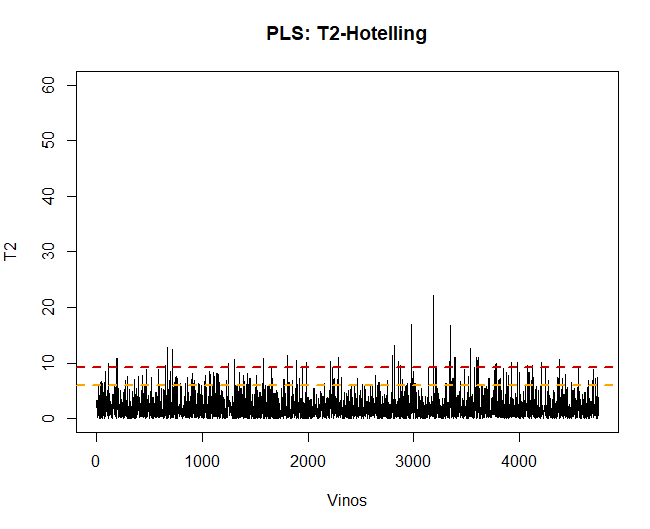
5.3.2 SCORE-PLOT
Una vez validados los datos, se pasa ya a la obtención del gráfico de scores, referente a los individuos. Se obtienen unos resultados muy similares a los obtenidos mediante el algoritmo del k-means utilizado en el Análisis 2. Los grupos no se separan de forma clara, la mayoría se superponen entre ellos. Tal y como se había comentado en el anterior análisis, esto podría ser debido a que los grupos no se separan por la calidad, sino por otras variables que en este análisis no se han dispuesto como pueden ser la denominación de origen del vino, el tipo de uva que se utiliza para su elaboración, etc.
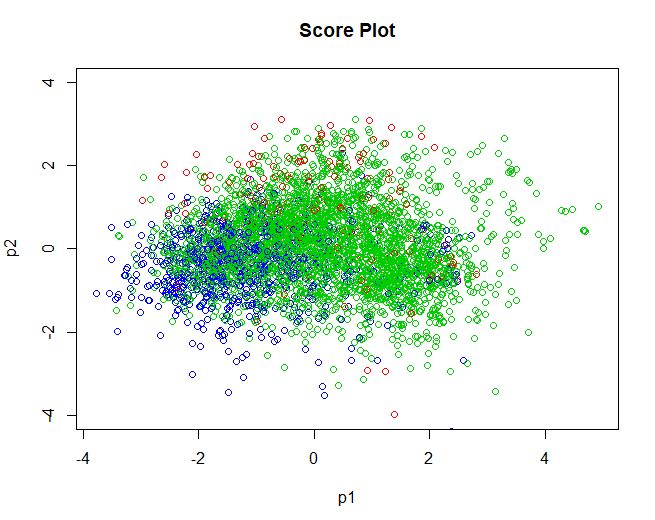
5.3.3 LOADING-PLOT
Por otra parte, se pasa a graficar el gráfico de loadings, referente a las variables. En este caso se obtienen unos resultados muy parecidos a los que se obtuvieron en el análisis de componentes principales. El azufre total, azufre libre y alcohol, tienen una alta contribución en las dos dimensiones. Sin embargo, utilizando PLS-DA se obtiene que el pH no contribuye en ninguna de las dos componentes (en PCA tenía una gran contribución en la segunda componente)
5.4 PREDICCIÓN DEL MODELO PLS-DA
En este cuarto apartado se realizará la predicción del modelo utilizado en este tercer análisis. Al disponer de unas 5000 observaciones, se pasa a crear un conjunto de entrenamiento y otro de test.
## PLS-DA
## 3800 samples x 11 variables and 1 response
## standard scaling of predictors and response(s)
## R2X(cum) R2Y(cum) Q2(cum) RMSEE pre ort pR2Y pQ2
## Total 0.307 0.0982 0.0937 0.338 2 0 0.05 0.05
5.4.1 CONJUNTO DE ENTRENAMIENTO
Utilizando los datos de entrenamiento, se puede observar que el modelo tiene un accuracy del 76,55%, lo cual es un valor muy aceptable. Sin embargo, hay que fijarse bien en las observaciones que predice para cada uno de los grupos. Dicho valor de precisión es alto debido a que clasifica bien a casi todos los vinos del grupo 2 (“buenos” con una valoración entre 5 y 7). Clasifica 2801 vinos en el grupo 2, y los 43 restantes al grupo 3.
No obstante, del primer grupo no ha clasificado bien a ninguno de estos (120 en el grupo 2 y 1 en el grupo 3). Finalmente, en el grupo 3 ha clasificado 108 observaciones pertenecientes a ese grupo y 727 para el grupo 2.
Por lo tanto, se puede decir que el modelo predice muy bien los vinos del segundo grupo. Como consecuencia, el valor de precisión es elevado.
## Confusion Matrix and Statistics
##
## mypred
## 1 2 3
## 1 0 120 1
## 2 0 2801 43
## 3 0 727 108
##
## Overall Statistics
##
## Accuracy : 0.7655
## 95% CI : (0.7517, 0.7789)
## No Information Rate : 0.96
## P-Value [Acc > NIR] : 1
5.4.2 CONJUNTO DE TEST
Finalmente, para validar el modelo, se realizará lo mismo de antes pero, en este caso, con observaciones que el modelo no ha visto anteriormente (conjunto de test)
Se puede observar una tendencia parecida a la del conjunto de entrenamiento. El modelo tiene una accuracy del 76,92%, valor muy similar al obtenido en el otro conjunto. Sin embargo, tal y como se ha comentado anteriormente, el modelo clasifica muy bien solamente a los vinos del grupo 2 pero los otros dos grupos no los distingue bien.
## Confusion Matrix and Statistics
##
## mypred
## 1 2 3
## 1 0 30 0
## 2 0 692 19
## 3 0 170 38
##
## Overall Statistics
##
## Accuracy : 0.7692
## 95% CI : (0.7411, 0.7957)
## No Information Rate : 0.9399
## P-Value [Acc > NIR] : 1
6 CONCLUSIONES
6.1 COMPARATIVA DE LOS MÉTODOS UTILIZADOS
Finalmente, en este proyecto se han utilizado tres métodos para los tres análisis correspondientes: Análisis de Componentes Principales, Clustering y Partial Least Squares – Discriminant Analysis (PLS-DA).
El primer método, el PCA, ha servido para obtener un preprocesado de los datos y de esta forma, poder estudiar la base de datos un poco más a fondo, analizando las variables que más contribución tienen en las principales dimensiones que se han obtenido. Se han podido encontrar resultados similares entre el PCA y el PLS-DA, esto es, analizando los loading-plot de ambas técnicas, se han obtenido las mismas variables que contribuían más en las dos técnicas, exceptuando algunas excepciones.
Por otra parte, el PCA, gracias a la limpieza que se ha realizado en la base de datos, ha servido para el segundo análisis, clustering, ya que ha permitido obtener los clústers de una forma más balanceada, sin grupos anómalos con pocas observaciones.
Finalmente, el método del PLS-DA, además de lo que se ha comentado anteriormente acerca de los resultados similares obtenidos con el PCA, se ha utilizado para evaluar la capacidad predictiva del modelo. Se ha obtenido un buen primer modelo pero que debería ser mejorado en un futuro, debido a que los grupos con menores observaciones no se predecían de forma correcta.
6.2 DISCUSIÓN SOBRE LOS MÉTODOS NO APLICADOS
En este proyecto no se han utilizado tres métodos: Análisis Factorial de Correspondencias (AFC), Reglas de Asociación y Análisis Discriminante. Las dos primeras técnicas no se han utilizado debido a que la base de datos que se ha utilizado para este trabajo no disponía de variables cualitativas (solamente la variable respuesta, calidad del vino). El hecho de transformar todas las variables podría haber provocado una pérdida importante de información.
Por otra parte, el análisis discriminante era también una buena opción para obtener las variables que más influenciaban a la hora de discriminar entre los distintos grupos en los que se clasificaban los vinos y posteriormente, clasificar nuevas observaciones. Ya se había aplicado PCA y clustering y, debido a que la realización del PLS era obligatoria, no se ha podido estudiar dicho método.
Finalmente, dentro del PLS se ha utilizado la técnica del PLS-DA debido a que la variable respuesta era cualitativa. De esta forma se ha utilizado dicha variable como Y y las demás variables físico-químicas como X.
7. OTROS TEMAS
7.1 COMENTARIOS SOBRE ARTÍCULOS LEÍDOS
Se ha podido estudiar que los distintos grupos no se separan bien por la calidad. Por lo tanto, visto esto, se decidió investigar un poco acerca de cómo podría ser esta agrupación. A través de algunas noticias y artículos se ha podido saber que la calidad del vino no es una combinación lineal de las variables físico-químicas de las que se disponía. Por lo tanto, la valoración de un vino no es lineal, tiene tendencias con errores. Dichos errores se ven influenciados por los criterios de cada juez.
Por lo tanto, la variable ‘quality’, en el caso de ser obtenida a partir de valoraciones de jueces expertos, tiene ciertas imprecisiones que son debidas a los gustos de cada uno de estos.
8. ANEXO
8.1 BIBLIOGRAFÍA
- Manual características de los vinos
- ¿Cómo saber si estoy disfrutando de un vino de calidad?
- HCPC
- Practical Guide To Principal Component Methods in R (Kassambara)
- FactoMineR
- ANALISIS DE DATOS MULTIVARIANTES – Daniel Peña
- THE ELEMENTS OF STATISTICAL LEARNING
8.2 ANÁLISIS DISTRIBUCIÓN DE LAS VARIABLES
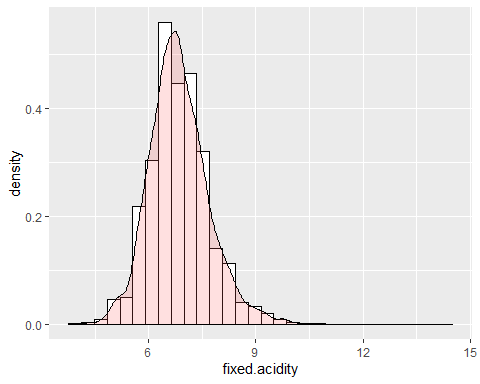
HISTOGRAMA ACIDEZ FIJA
La primera de las variables es la acidez fija. Dicha variable tiene una asimetría de 0.647 pero una kurtosis de 5.16. Esto indica que dicha variable no sigue una distribución normal. Aparte se observa un dato extremo el cual toma el valor de 14,2.
HISTOGRAMA ACIDEZ VOLÁTIL
La acidez volátil tiene una forma similar a la anterior variable. Dicha variable tiene una asimetría de 1,576 y una kurtosis de 8,08 la cual indica también que no sigue una distribución normal.
Se observa que las dos anteriores variables tienen colas largas y positivas y, debido a esto, la media es mucho más alta que lo que debería ser. 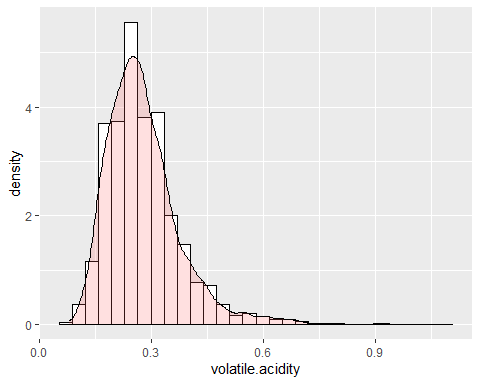
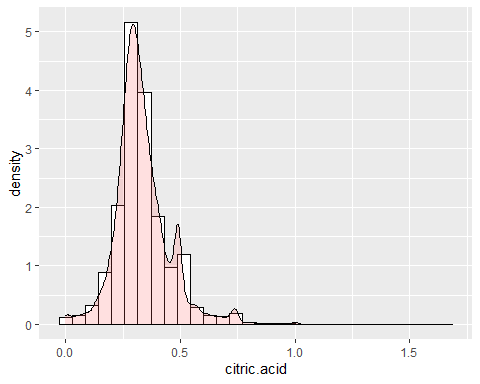
HISTOGRAMA ÁCIDO CÍTRICO
En el ácido se pueden observar algunos datos atípicos como por ejemplo 1,66 g/dm^3 que marca el máximo de la variable. Aparte de esto, se obtiene una asimetría de 1,28 y una curtosis de 9,16. Por lo tanto, tampoco sigue una distribución normal.
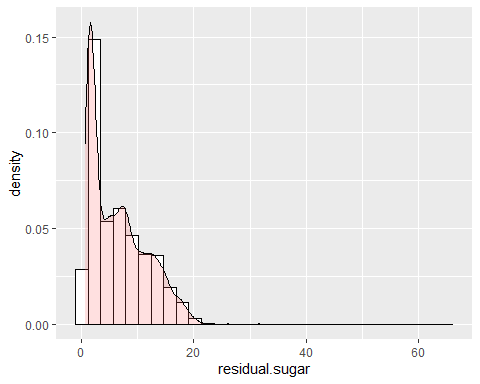
HISTOGRAMA AZÚCAR RESIDUAL
El azúcar residual tiene un sesgo positivo. Se observa que tiene una asimetría de 1,07 y una curtosis de 6,46, es decir, no sigue una distribución normal. Se observa un pico muy elevado.
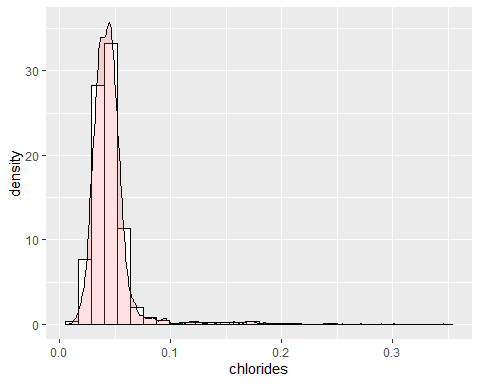
HISTOGRAMA CLORO
El cloro tiene varios datos extremos con un coeficiente de curtosis de 40,52. Además tiene una asimetría positiva con un coeficiente de 5,02. Por lo tanto dicha variable no se distribuye según la campana de Gauss.
HISTOGRAMAS DIÓXIDOS DE AZUFRE TOTAL Y LIBRE
Las distribuciones para el dióxido de azufre, tanto el libre como el total, son simétricas debido a que tienen unos coeficientes de asimetría de 1,40 y 0,39 respectivamente. En los dos casos existen datos extremos (curtosis de 14,45 y 3,57). No siguen una distribución normal. 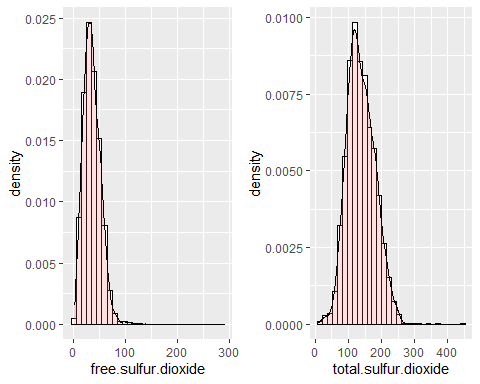
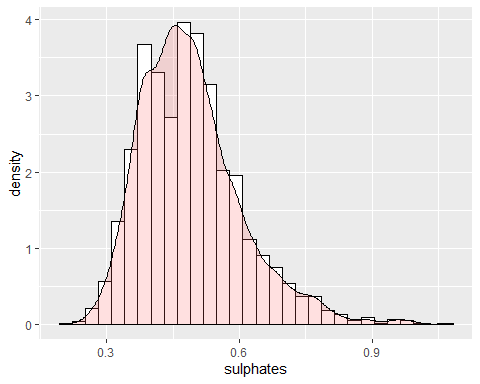
HISTOGRAMA SULFATOS
El sulfato tiene una asimetría positiva con un coeficiente de 0.9768. Como tiene un coeficiente de curtosis superior a 2, existen datos anómalos y, por tanto, no sigue una campana de Gauss.
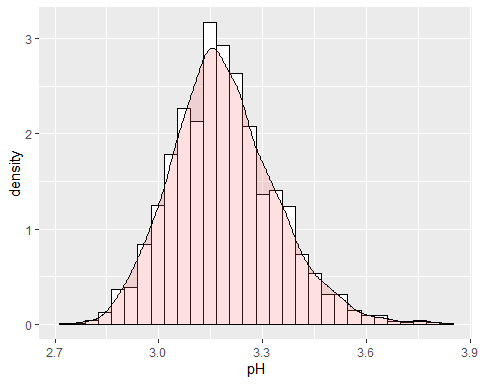
HISTOGRAMA PH
El pH del vino se encuentra alrededor de 3,15 con algunos datos anómalos debido a que el coeficiente de curtosis es superior a 2.