Aplicación de métodos estadísticos y predictivos
(FAMD, Clustering y PLS-DA)
sobre datos del cardiovasculares para obtener que variables causan problemas del corazón.
Angel Langdon & Ignacio Cano
1. Descripción del estudio y de la base de datos.
1.1 Descripción del estudio
En este estudio se va a realizar un análisis de la relación entre unas variables que indican propiedades físicas del estado de una persona (detalladas más adelante) y el hecho de tener o no un problema del corazón. De esta forma, se obtendrán cuales son las variables más significativas a la hora de determinar si una persona tiene un problema del corazón. Además, se intentará clasificar a los individuos según su estado físico en dos grupos, si han sufrido un problema del corazón o no. También se estudiará la posibilidad de predicción mediante un modelo PLS-DA.
1.2 Descripción de la base de datos
La base de datos consta 14 variables y 303 observaciones. Las variables que manejamos son comunes y fáciles de entender. En su mayoría tratan aspectos técnicos de propiedades del corazón y de niveles de ciertas sustancias que son influyentes a la hora de determinar la existencia de una enfermedad del corazón. A continuación, se explican las 14 variables para una mayor claridad a la hora realizar el análisis, además que es imprescindible conocer de qué trata el tema para realizar un buen análisis.
- Edad: La edad de la persona en años
- Sexo: El sexo de la persona (1 = macho, 0 = hembra)
- Dolor_pecho: El tipo de dolor de pecho experimentado
- Valor 0 –> Angina típica
- Valor 1 –> Angina atípica
- Valor 2 –> Dolor de pecho pero no de tipo angina
- Valor 3 –> Dolor asintomático
- (Angina = dolor de carácter opresivo causado por insuficiente aporte de sangre <> a las células del corazón)
- p_sanguinea_mmHg: La presión sanguínea en reposo de la persona medida mm Hg al ingreso al hospital
- colesterol: El nivel de colesterol de la persona medido en mg/dl
- hiperglucemia: El nivel de glucemia (glucosa libre en sangre) en ayuno de la persona (>120mg/dl, 1 = true ; 0 = false). Si es mayor que 120mg/dl se denomina hiperglucemia, y si el paciente tienen hiperglucemia durante mucho tiempo contribuye al desarrollo de diabetes.
- electro_reposo: Un electrocardiograma en reposo de la persona
- Valor 0 –> normal
- Valor 1 –> Anormalidad en la onda del segmento ST-T (asociado con diversos problemas del corazón según el tipo de anormalidad)
- Valor 2 –> Hipertrofia en el datatrículo izquierdo (provocado por alta presión arterial, puede causar un ataque al corazón)
- latidos_minuto: La pulsaciones por minuto más altas registradas por la persona
- angina_por_ejercicio: Si la angina ha sido producida por ejercicio (1 = sí; 0 = no)
- s_st: se estudia la depresión del segmento ST provocada por ejercicio físico en comparación a la depresión del segmento ST cuando el paciente está en reposo. Cuanto mayor sea este valor más probabilidad de sufrir un problema del corazón.
- pendiente_s_st: la pendiente del segmento ST en el pico de ejercicio
- Valor 1 –> Pendiente positiva
- Valor 2 –> Pendiente plana
- Valor 3 –> Pendiente negativa
- Sería interesante cambiar estos valores a 1, 0 y -1 respectivamente para que sean un poco más similares a lo que representan.
- n_vasos_sanguineos: número de vasos sanguíneos principales (0-3)
- defecto_tipo: Es un test hecho con un elemento radioactivo (Thalium) inyectado en el corriente sanguíneo de los pacientes. Esto permite estudiar el corriente sanguíneo tanto en reposo como haciendo ejercicio:
- Valor 3 –> Corriente sanguíneo normal.
- Valor 6 –> No se observa corriente sanguíneo por la zona ni en reposo ni haciendo ejercicio. (defecto fijo)
- Valor 7 –> No se observa corriente sanguíneo por la zona haciendo ejercicio pero sí en reposo. (defecto reversible)
- problema_corazon: Problema del corazón:
- Valor 0 –> No
- Valor 1 –> Sí
- Valor 2 –> Sí, peor
- Valor 3 –> Sí, mucho peor
- Valor 4 –> Sí, lo peor posible
- Cabe resaltar que la variable problema_corazon nos servirá como referencia para saber si podemos llegar a predecir posibles casos de problemas al corazón a partir de los valores que tomen los individuos en el resto de variables. Por ello esta variable se tomará como suplementaria y nos servirá como referencia.
2. Análisis exploratorio inicial y pre-proceso de los datos
2.1 Datos faltantes
Revisamos que no hayan datos faltantes, para ello se muestra un gráfico de datos faltantes según variable
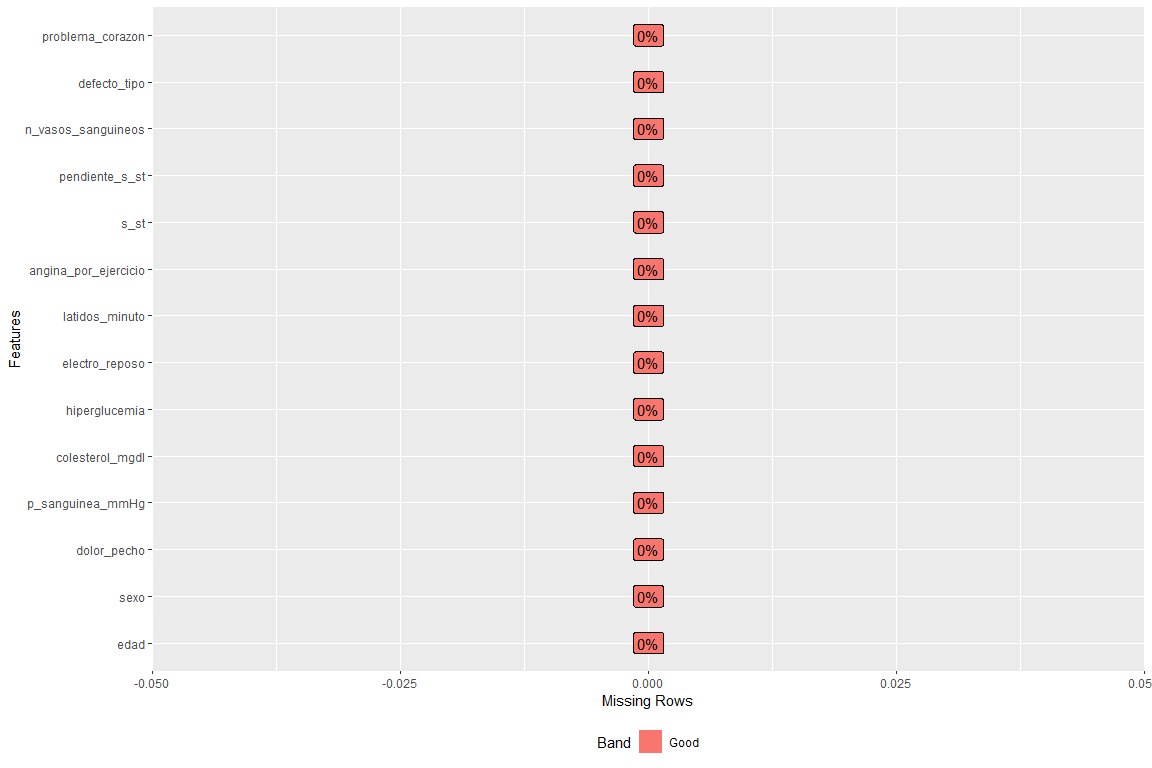
Cómo se puede observar no hay ningún campo vacío en ninguna variable.
2.2 Variables y/o registros descartados.
Realizando un poco de investigación, este dataset en la columna de número de vasos sanguíneos algunas observaciones toman el valor ?, el cual está mal. (En el dataset original representan NaNs). Lo mismo ocurre con la variable defecto_tipo, que toma el valor ?, está mal. Por ello eliminaremos dichas observaciones
2.3 Recodificación de las variables
Este paso se realiza con el fin de obtener unas categorías que sean más descriptivas. De esta forma categorías que antes eran “1” y “0” pasarán a ser hombre y mujer respectivamente.
2.4 Distribución de las variables
Este paso lo realizamos con el fin de observar que valores toman las variables y también para asegurarnos de que no existen valores erróneos.
En el Anexo 8.2: Análisis distribución de las variables está todo explicado
Una vez realizado el estudio de la distribución de las variables, observamos ninguna de ellas tiene valores erróneos, y por lo tanto, podemos continuar con el análisis.
3. Análisis 1 FAMD(factominer)
FAMD (Análisis de factores de datos mixtos) es un método de componentes principales dedicado a explorar datos con variables continuas y categóricas. A groso modo se trata de un mezcla de PCA y AFC.
En concreto, las variables continuas son escaladas a la varianza unitaria y las variables categóricas son transformadas a un tabla disyuntiva y luego escaladas utilizando un criterio de AFC. Esto hace que ambos tipos de variables sean representativas en el análisis. Es decir, que un tipo de variables no influencien más que el otro tipo de variables. En este caso, se va a dejar como variable suplementaria ‘problema corazón’, de forma que podamos ver si sin su presencia los individuos se distribuyen en dos grupos tal y como harían si estuviera presente dicha variable. Si se desea buscar más información sobre FAMD se puede hacer en http://www.sthda.com/english/articles/31-principal-component-methods-in-r-practical-guide/115-famd-factor-analysis-of-mixed-data-in-r-essentials/ y también en https://rdrr.io/cran/FactoMineR/man/FAMD.html
3.1 Objetivos
- Realizar preprocesado de los datos que son numéricos y categóricos para obtener su matriz de scores (con las X componentes principales más significativas) con el objetivo de poder utilizarla en Clustering (clustering no admite datos mixtos)
- Estudiar las relaciones entre las variables del estado físico de una persona dejando como suplementaria la variable problema corazón para que no influya en el estudio y ver si los individuos, por sí solos, se distribuyen en dos grupos (con problema de corazón sí o no).
3.2 Aplicación del método y resultados numéricos y gráficos
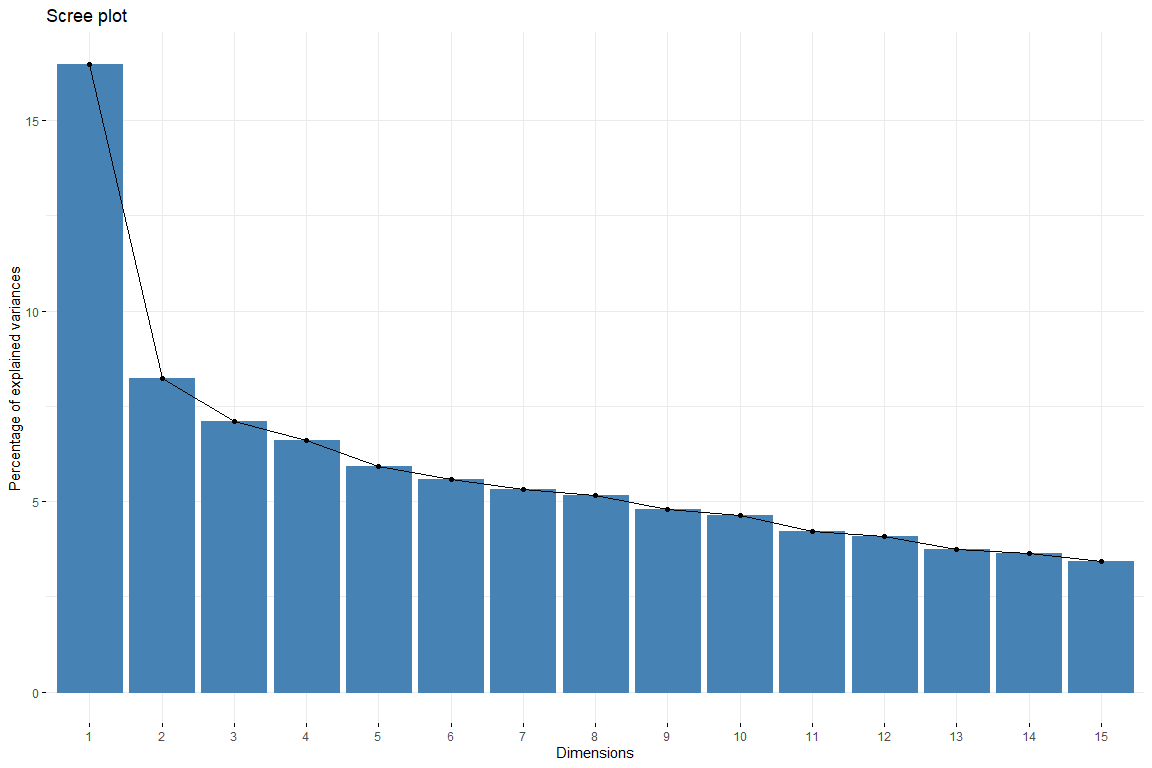
En el scree plot podemos observar cómo a partir de la 6 dimensión la aportación de las dimensiones desciende de manera uniforme. Por lo tanto, se escogerán 6 dimensiones para representar nuestros datos. También cogemos 6 dimensiones ya que así conseguimos una explicación del 50% de la variabilidad. Ahora vamos a estudiar la aportación de las variables a las primeras dimensiones.
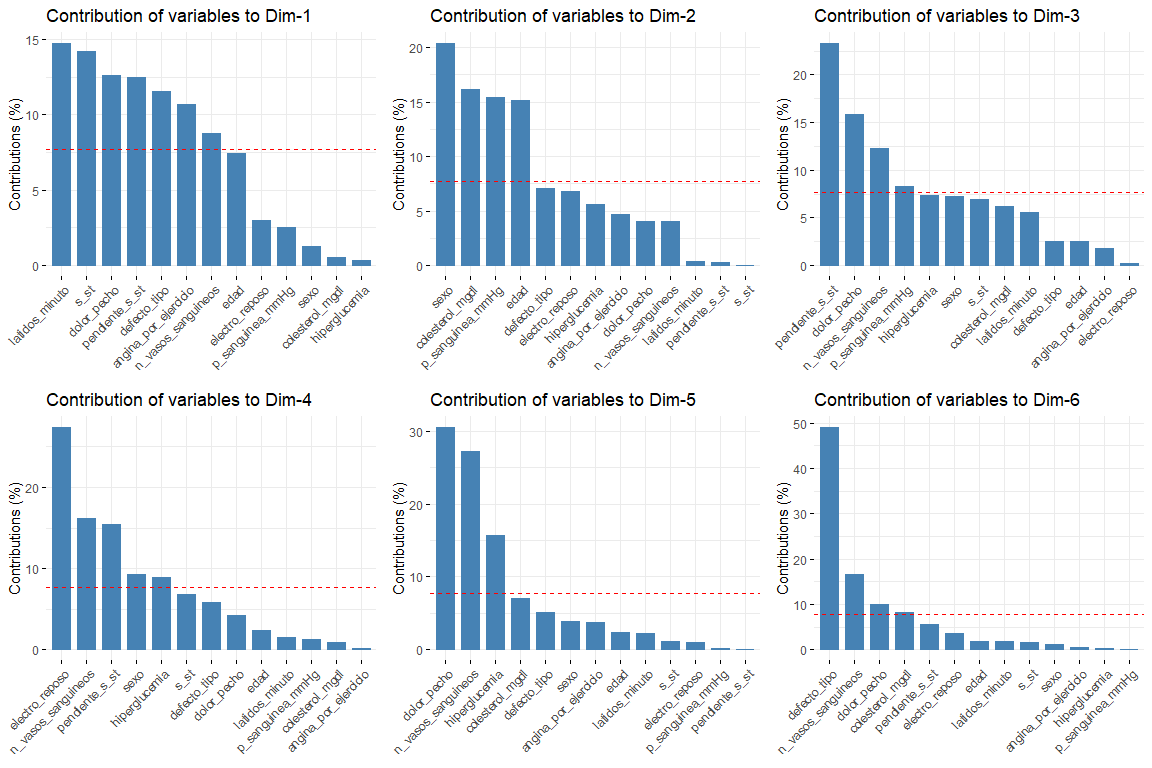
Los resultados más interesantes de las contribuciones son los de las dos primeras dimensiones (ya que son las que más variabilidad explican). Cabe destacar que la primera dimensión la caracterizan varias variables (lógico ya que es la que más variabilidad explica de todas) estas son defecto_tipo, dolor_pecho y st. En la segunda dimensión, el número de variables que caracterizan esta dimensión es menor con respecto a las de la primera dimensión, y estas son sexo, edad, colesterol_mgdl, p_sanguinea_mmHg. Una vez caracterizadas las dos primeras dimensiones, vamos a ver el gráfico de variables dibujadas en el espacio vectorial de las dos primeras dimensiones, para así poder observar las relaciones entre variables, y su caracterización en cada una de las dos dimensiones de forma más visual.
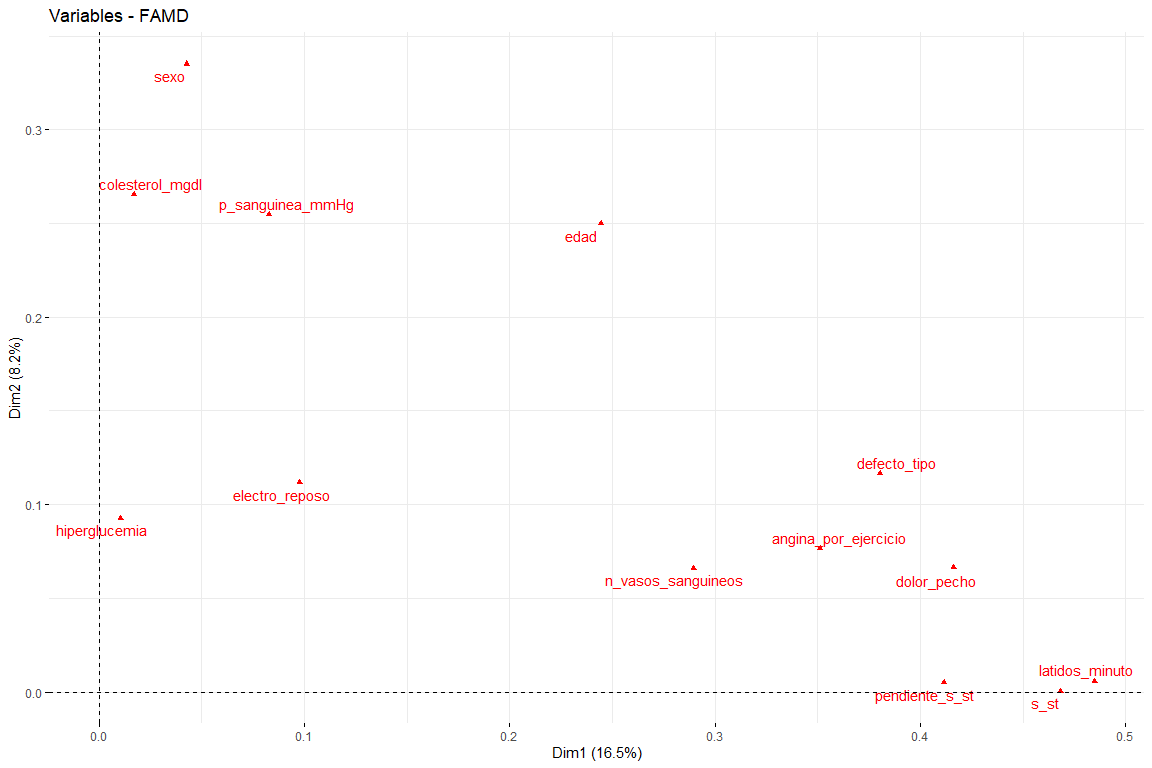
En este gráfico podemos ver representadas las dos primeras dimensiones (las más importantes) y tenemos resultados que confirman los vistos en el gráfico de contribuciones. Variables como latidos_minuto o s_st son las que más contribuyen a la primera dimensión y las variables sexo o edad tienen una gran contribución a la segunda dimensión.
3.3 Discusión de los resultados
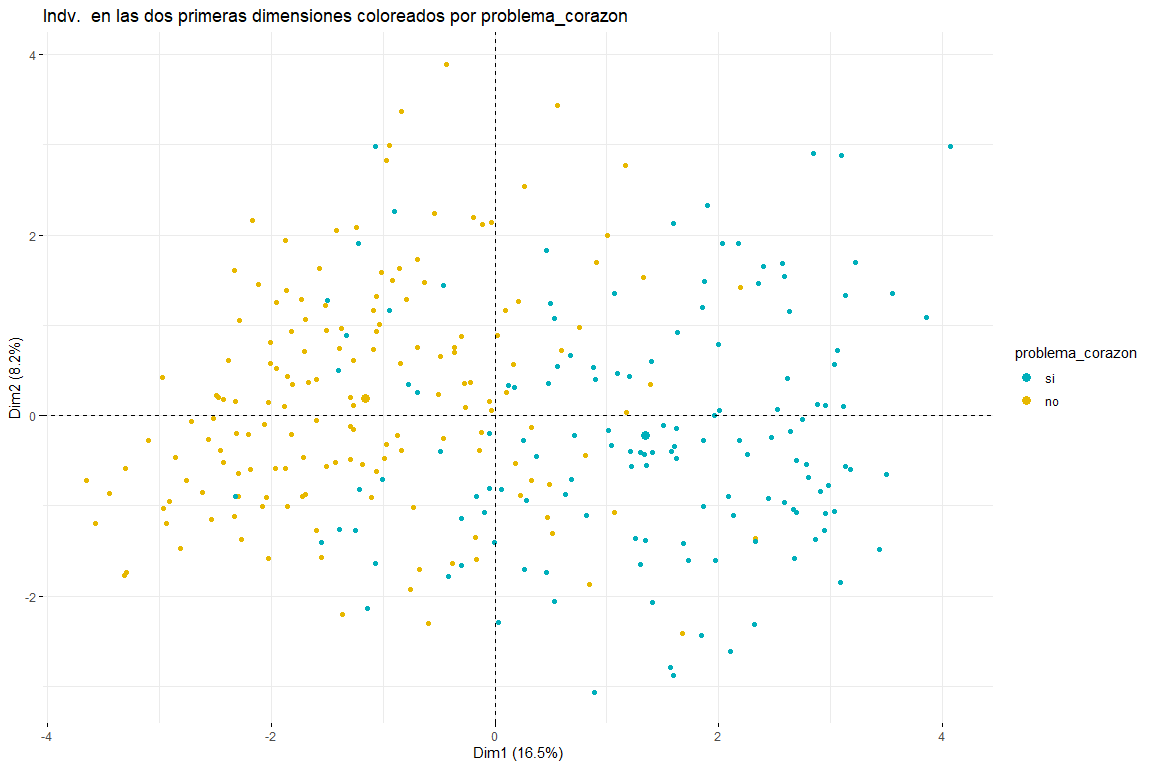
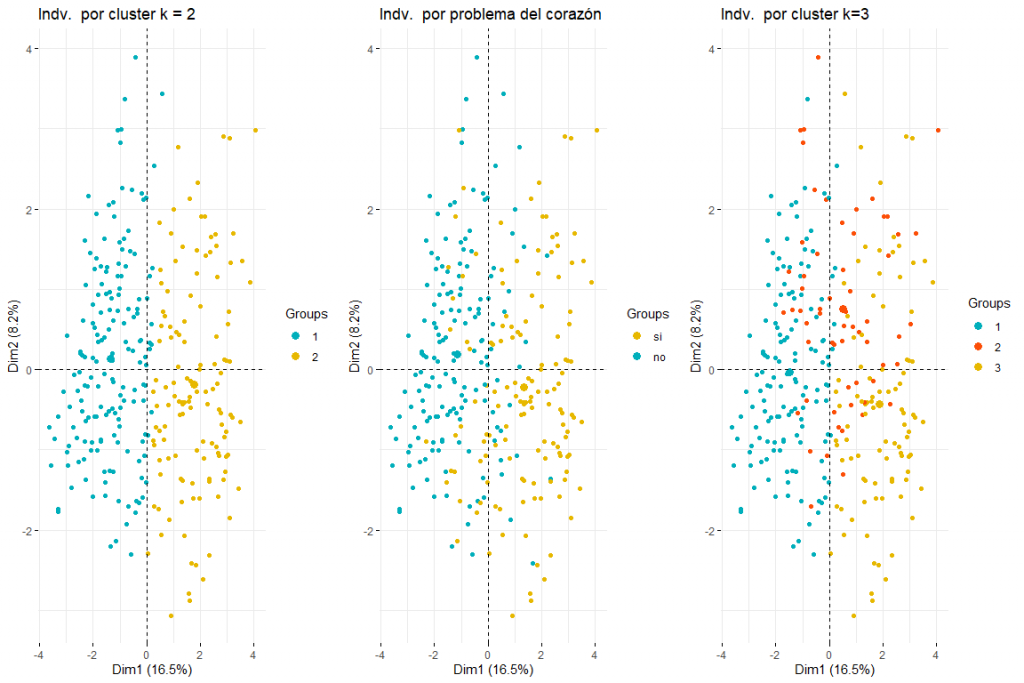
Tras ver el gráfico de individuos coloreados por problema_corazon podemos distinguir entre dos y tres grupos (para ello habría que hacer unos posteriores análisis de clústering) ambos posibles resultados tienen sentido ya que dos grupos implicaría que los valores en determinadas variables (defecto_tipo, dolor_pecho, sexo, edad, colesterol_mgdl, p_sanguinea_mmHg) implican la separación entre los casos de problemas al corazón y los que no. Tres clústers podrían tener sentido también ya que viendo el gráfico vemos como se separan los los valores problema_corazon = si y problema_corazon = no, pero también podemos ver como en el centro se mezclan los valores de problema corazón si y problema corazón no, por lo cual la presencia de tres clústeres también podría ser posible. También podemos afirmar que la principal dirección de separación de los grupos viene debido a la primera dimensión, por tanto las variables defecto_tipo, dolor_pecho, s_st, defecto_tipo, p_sanguinea_mmHg serían aquellas que permitirían identificar aquellos pacientes que han sufrido un problema del corazón. También parece que los individuos que han tenido problema del corazón no solo están desplazados hacia la derecha sino que también hacia abajo. Esto implicaría que variables que más contribuyen a la segunda dimensión (sexo, edad, colesterol_mgdl, p_sanguinea_mmHg) también tendrían relación con identificar si un paciente ha tenido un problema del corazón o no. Estas conclusiones se espera que se puedan confirmar con el posterior análisis de clustering a partir de este análisis de FAMD.
4. Clustering jerárquico
El HCPC (Hierarchical Clustering on Principal Components) es un algoritmo que agrupa individuos similares en clusters pero con una peculiaridad. Está hecho para trabajar con los resultados de un método de componentes principales (PCA, MFA, FAMD…). Para más información: http://www.sthda.com/english/articles/31-principal-component-methods-in-r-practical-guide/117-hcpc-hierarchical-clustering-on-principal-components-essentials/
4.1 Objetivo
- A través de la matriz de scores obtenida en el FMAD observar si realizando clustering jerárquico con estos individuos se obtienen dos clusters que agrupan a los individuos en personas con y sin problema del corazón. En caso de que esto no ocurra, estudiar el porqué de la existencia del número de clusters inesperado.
4.2 Aplicación del método
Para hacer el clústering vamos a usar las coordenadas de los individuos en las 6 dimensiones que hemos cogido en el FAMD. El objetivo del FAMD, como se ha comentado anteriormente, era realizar un preprocesado de los datos para poder realizar posteriormente clústering. A pesar de todo, hemos obtenido resultados bastante reveladores con el FAMD solamente y se espera que con el análisis de clústering estos resultados terminan de confirmarse.
Para el cálculo de la matriz de scores que posteriormente se utilizará en el clustering, se van a utilizar todas las variables que indican el estado físico de la persona. Se recalca que en el clustering jerárquico NO se va a incluir la variable problema_corazón para que éste no tenga efecto a la hora de calcular los clusters. Ya que el objetivo es calcular clusters a través de las variables del estado físico, para observar si guarda relación con el problema del corazón.
4.2.1 Calculamos las distancias y el estadístico Hopkins
Antes de aplicar cualquier algoritmo de clustering es importante preguntarse si existe algún tipo de agrupación para ello, realizamos el estadístico de Hopkins que nos indica si existe agrupación en los datos. Debemos recordar que la librería ‘clustertend’ devuelve 1-H siendo H el estadístico de Hopkins.
$H
## [1] 0.2628502
En el caso de los datos de corazón el estadístico tiene un valor de 0.26 muy lejano del 1, por tanto, podemos afirmar que existe agrupación en nuestros datos.
4.2.2 Número óptimo de clusters
Para poder ejecutar el algoritmo de Clustering jerárquico, hemos de saber el número óptimo de clusters. Para ello ejecutaremos los siguientes tests.
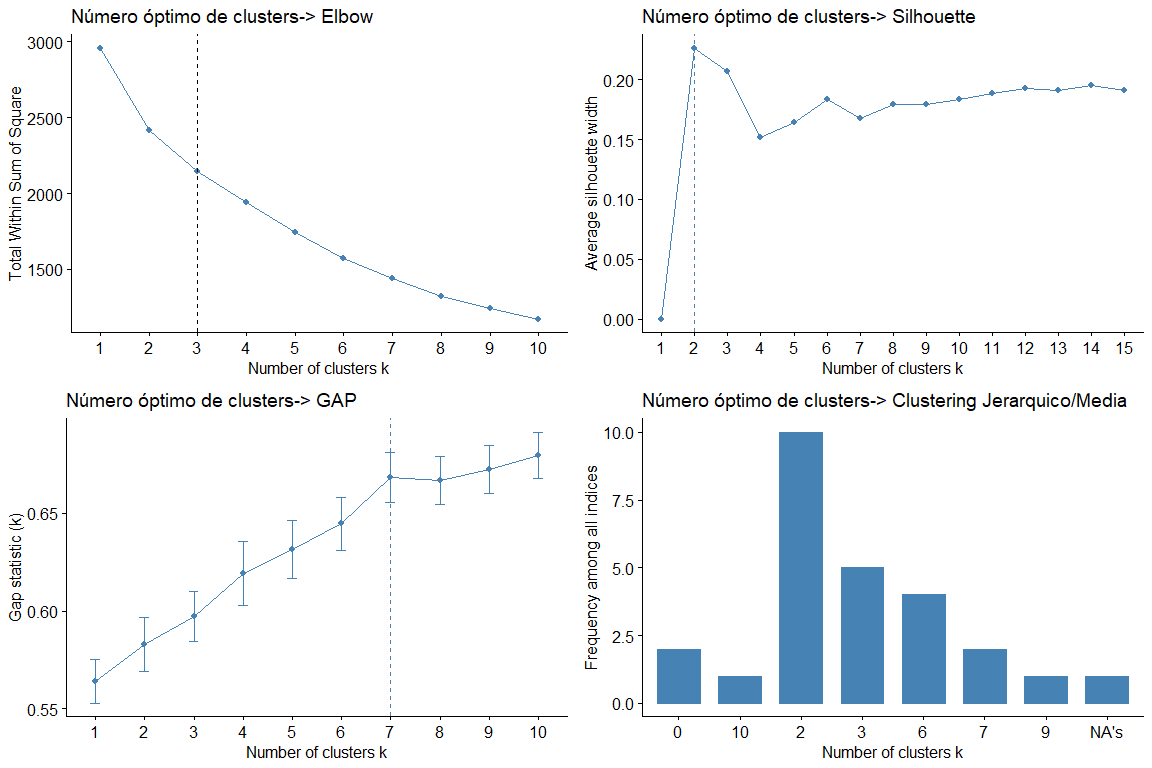
Observando las gráficas y las tablas podemos observar que para los diferentes estadísticos y métodos obtenemos diferentes valores de clusters. El resultado más frecuente es considerar 2 clusters, seguido de 3 clusters. (el resultado 7 también aparece repetido pero como no tendría sentido considerar 7 grupos desechamos esta conclusión)
A continuación, realizamos un cluster plot de 2 y 3 clusters respectivamente para ver cual es el que mejor se ajusta a nuestros datos. Utilizamos para obtener los datos kmeans puesto que al analizar los datos podemos ver que los datos no tienen valores muy extremos y por tanto, no es necesario utilizar métodos más robustos como PAM, por ejemplo.
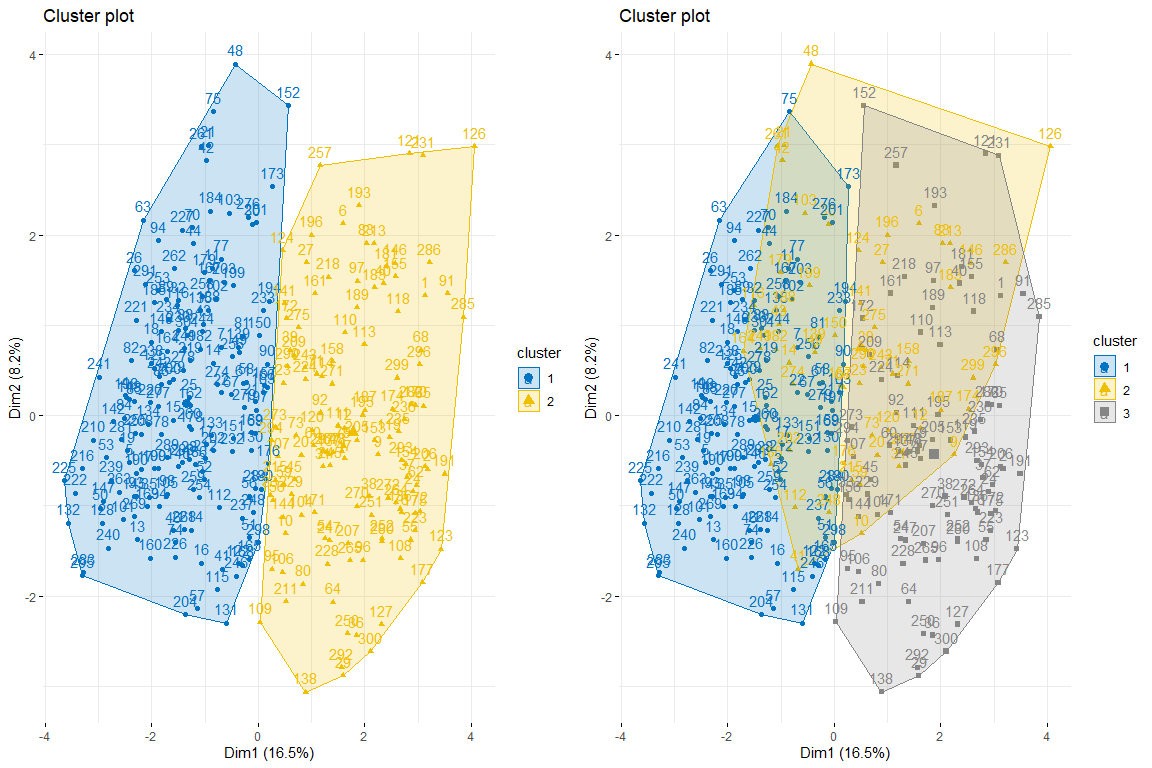
Como podemos observar 2 clusters parece ser la mejor opción ya que crea 2 grupos bastante naturales, es decir, aquellos individuos con problemas de corazón y aquellos que no.
Vamos a continuar con la comparación entre dos y tres clusters coloreando los individuos del plot de individuos de FAMD.
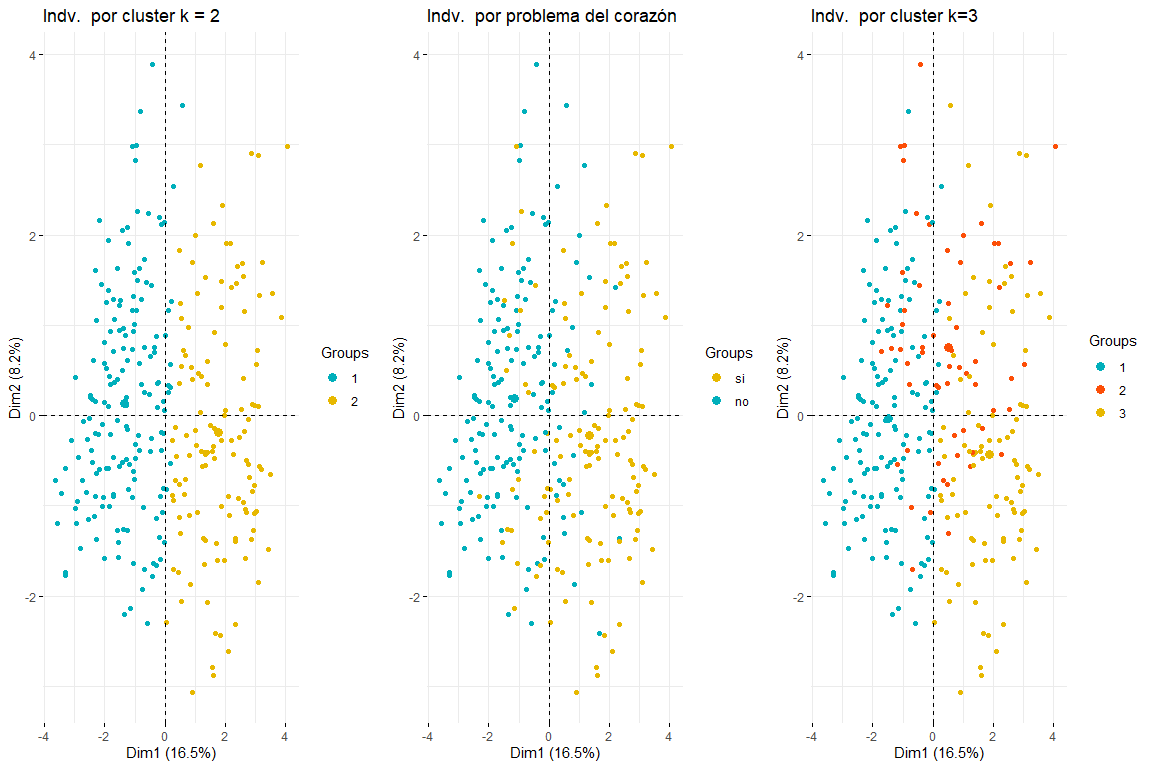
Como se puede observar el los tres gráficos de los individuos coloreados por cluster y por problema del corazón, se aprecia que dos clusters es el que mejor se adapta, y más se parece a el gráfico de individuos coloreados por problema del corazón. Después de comparar estos tres grupos de gráficos podemos llegar a la conclusión que usar dos clusters se corresponde más con la distribución de los datos según problema_corazón. Por todo ello, se elegirán dos clusters para el clustering jerárquico.
4.3 Resultados numéricos y gráficos
Por último se va a estudiar la relación entre las variables y los dos clusters y, por lo tanto, la relación de las mismas con el hecho de tener problema de corazón o no. Empezaremos con la relación entre las categorías de las variables cualitativas y la pertenencia a un clúster o a otro. Es evidente que aquellas categorías más relacionadas con un clúster son aquellas con un v.test más alto, mientras que aquellas cuyo valor de v.test sea muy negativo menos relacionadas estarán con dicho clúster (y como solo tenemos dos clusters probablemente dichas categorías con v.test muy negativo tendrán relación con el otro clúster).
res.hcpc2$desc.var$category
## $`1`
## p.value v.test
## pendiente_s_st=positiva 2.930295e-25 10.384064
## angina_por_ejercicio=angina_no_ejercicio 1.061236e-23 10.035774
## defecto_tipo=normal 2.733441e-22 9.709997
## n_vasos_sanguineos=0 4.846452e-13 7.229537
## dolor_pecho=angina_atipica 4.782592e-11 6.577551
## dolor_pecho=dolor_no_angina 1.569061e-07 5.244266
## sexo=mujer 4.235184e-05 4.094260
## electro_reposo=normal 4.769950e-03 2.822173
## $`2`
## Cla/Mod Mod/Cla Global
## p.value v.test
## angina_por_ejercicio=angina_ejercicio 1.061236e-23 10.035774
## pendiente_s_st=plana 5.739929e-20 9.149120
## dolor_pecho=asintomatico 8.164639e-19 8.857749
## defecto_tipo=defecto_reversible 2.547142e-15 7.911300
## sexo=hombre 4.235184e-05 4.094260
## n_vasos_sanguineos=2 4.952918e-05 4.057838
## n_vasos_sanguineos=3 9.157912e-05 3.911883
## defecto_tipo=defecto_fijo 1.073890e-04 3.873260
## n_vasos_sanguineos=1 4.649990e-03 2.830331
## electro_reposo=hipertrofia_izq 2.225498e-02 2.285988
## electro_reposo=anormalidad_st 3.297443e-02 2.132394
## pendiente_s_st=negativa 4.472770e-02 2.007206
Ahora se observará la relación entre las variables cuantitativas y los dos clusters. Las variables más representativas son aquellas con v.test más alto (en valor absoluto) y fijándonos en la diferencia entre ‘Mean in category’ y ‘Overall mean’ podemos hacernos una idea de qué valores toman en dichas variables los individuos que pertenecen a un clúster.
## $`1`
## v.test Mean in category Overall mean sd in category
## latidos_minuto 10.133353 161.3313609 149.597973 16.6608075
## p_sanguinea_mmHg -3.346967 128.6508876 131.648649 16.2372212
## edad -6.575012 51.5147929 54.513514 8.9085469
## s_st -9.798909 0.4757396 1.051351 0.6908983
##
## $`2`
## v.test Mean in category Overall mean sd in category
## s_st 9.798909 1.817323 1.051351 1.222434
## edad 6.575012 58.503937 54.513514 7.537699
## p_sanguinea_mmHg 3.346967 135.637795 131.648649 18.848618
## latidos_minuto -10.133353 133.984252 149.597973 20.744028
Así pues, se puede ver que los individuos que forman el primer clúster vienen definidos por tener unos valores altos en latidos_minuto (con respecto a la media), bajos en edad, p_sanguinea y s_st. También podemos ver cómo los individuos del cluster 1, es decir aquellos casos que no han sufrido un problema de corazón, son mujeres, cuyo dolor de pecho no es una angina o angina atípica y no provocada por el ejercicio. Además, su electro en reposo es normal, su valor tras el test con Thalium es normal y su n_vasos_sanguíneos es 0.
Por el otro lado, los individuos del segundo clúster son predominantemente hombres, cuya presión sanguínea es mayor que la media, cuyos latidos por minuto son menores que los de la media y cuyo s_st es mayor que la media. Destacan además por tener una pendiente_st plana, unos valores de 1, 2 o 3 en n_vasos_sanguíneos, cuya angina es provocada por ejercicio, su dolor es asintomático y su valor tras el test con Thalium es reversible o fijo. Por último sus valores de electro en reposo son hipertrofia o anormalidad_st.
4.4 Discusión de los resultados
Como se puede observar las variables que más caracterizan los clusters y de forma consecuente, también si una persona tiene problema de corazón o no, son aquellas variables que mayor contribución realizaban a la primera y segunda dimensión del FAMD hecho anteriormente. Además, podemos observar que las conclusiones que se han obtenido tienen sentido; los que han sufrido un problema del corazón (pertenecientes al cluster 2) tienen una media de latidos por minuto máxima muy baja, una edad avanzada, son varones, una presión sanguínea más elevada de lo normal, un dolor de pecho asintomático… todo esto son factores de riesgo para sufrir problemas cardiovasculares.
5. Análisis 3: PLS-DA
La regresión de mínimos cuadrados parciales o Partial least squares regression (PLS regression) es un método estadístico que tiene relación con la regresión de componentes principales, en lugar de encontrar hiperplanos de máxima varianza entre la variable de respuesta y las variables independientes, se encuentra una regresión lineal mediante la proyección de las variables de predicción y las variables observables a un nuevo espacio. Debido a que tanto los datos de X e Y se proyectan a nuevos espacios, la familia de los modelos PLS se conoce como factor de modelos bilineales. En nuestro caso, usaremos los cuadrados mínimos parciales Análisis discriminante (PLS-DA) que son una variante que se utiliza cuando la Y es binaria.
5.1 Objetivos
Existen dos objetivos a la hora de realizar el PLS-DA:
El primero consiste en comparar los resultados obtenidos en el FAMD mediante los gráficos de scores y loadings y ver si se puede interpretar el mismo resultado. También mediante el gráfico de Observation Diagnostics podremos observar la existencia o no de datos extremos.
El segundo objetivo es evaluar la capacidad predictiva del modelo PLS-DA con los datos, los cuales se separarán en datos de entrenamiento y datos de test. Esto servirá para ver si es posible predecir nuevos casos de problema al corazón con las variables disponibles.
5.2 Aplicación del método
Para la aplicación del método se ha utilizado un preproceso distinto de las variables ‘independientes’ que formarán nuestra matriz X, ya que la función opls necesita que todas las columnas de la matriz X sean de tipo ‘numeric’ (código disponible en Anexo)
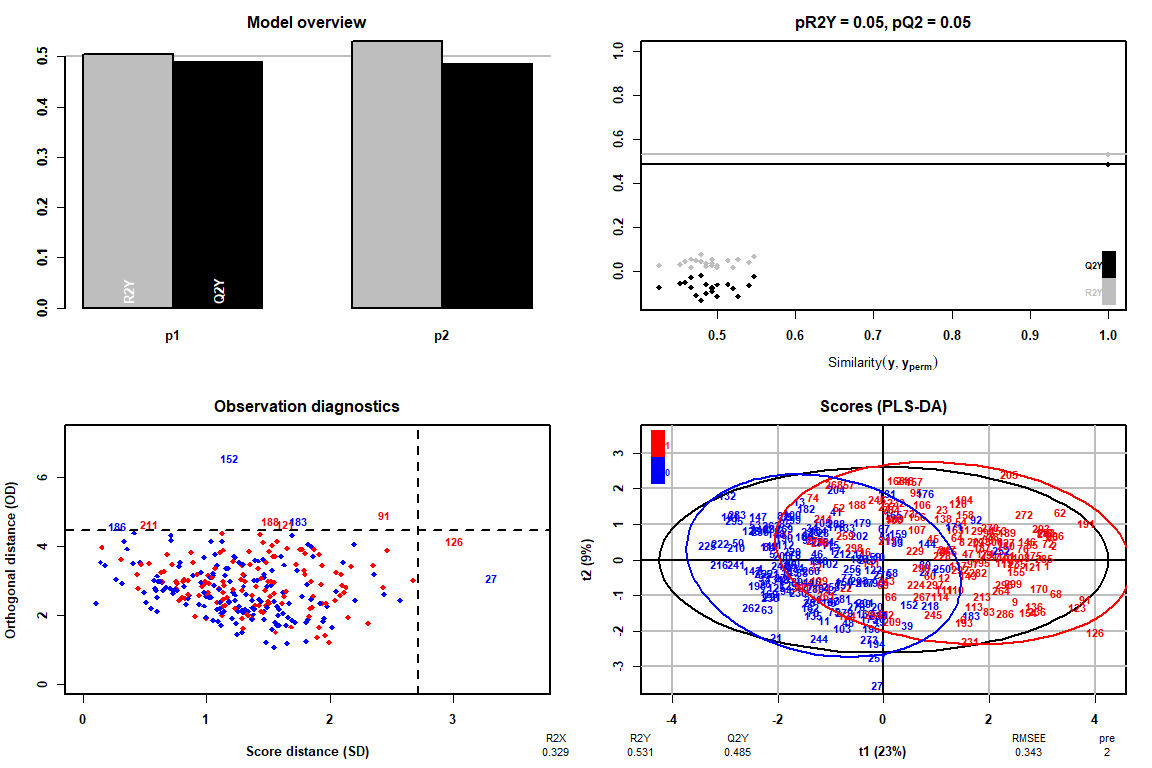
Cómo se puede observar gracias al gráfico de Observation Diagnostics, no existen valores extremos, por lo tanto podremos seguir el análisis del PLS-DA sin tener que eliminar ningún valor.
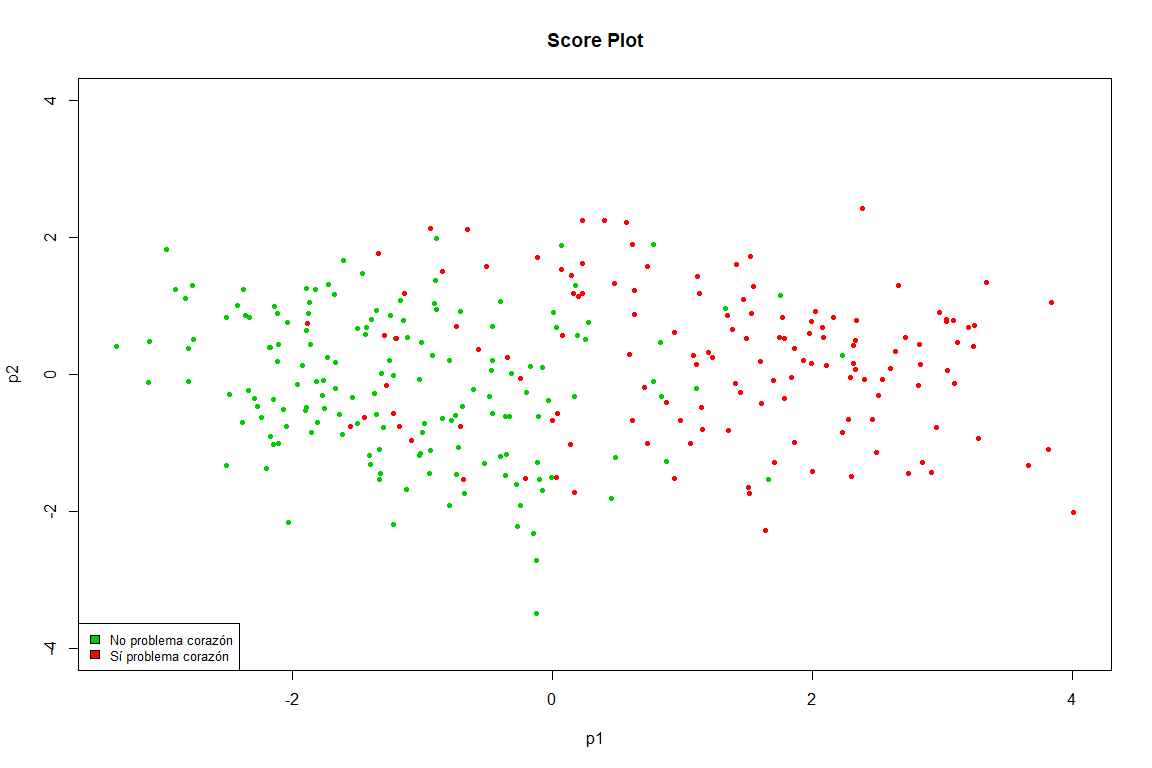
Este gráfico es prácticamente un calco del obtenido en el FAMD, vemos como claramente se separan en dos grupos los puntos (problema de corazón y no problema de corazón)
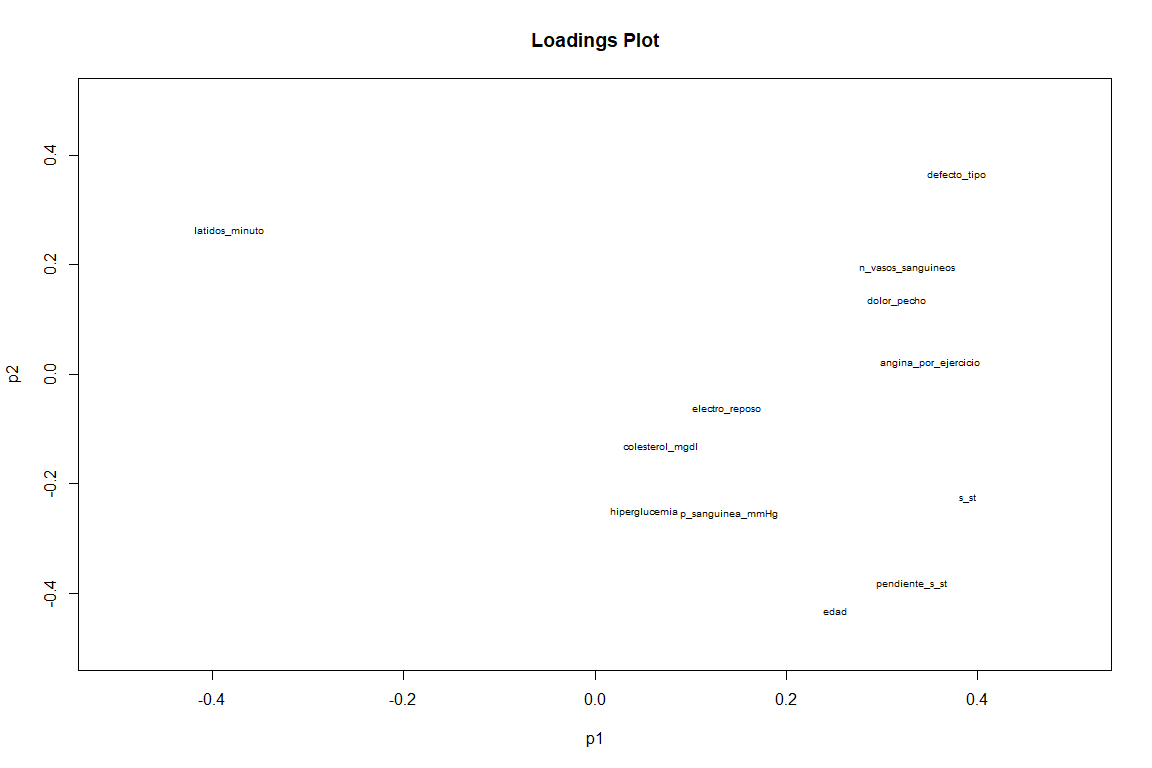
En el gráfico de Loadings, si vemos un resultado un tanto distinto al gráfico de loadings de FAMD. Vemos como variables como pendiente_s_st, defecto_tipo y latidos_minuto (aunque ésta con valor negativo ) tienen una gran contribución a las dos componentes. Mientras que variables como angina_por_ejercicio y dolor_pecho contribuyen sobretodo a la primera componente.
Ahora pasamos a analizar la capacidad predictiva del pls-da mediante datos de entrenamiento y datos de test.
mypred = predict(myplsda)
confuTrain = table(trainDatos$problema_corazon, mypred)
confusionMatrix(confuTrain)
## Confusion Matrix and Statistics
## mypred Accuracy : 0.8487
## 0 1 Kappa : 0.6946
## 0 113 15
## 1 21 89 Balanced Accuracy : 0.8495
Como podemos ver el modelo prediciendo sus propias filas, tiene un accuracy de 0.85, valor muy bueno que viene respaldado por un kappa 0.7, el cual indica una buena concordancia de nuestros datos. (https://es.wikipedia.org/wiki/Coeficiente_kappa_de_Cohen)
Lo siguiente es intentar predecir datos que el PLS-DA nunca ‘ha visto’
mypred = predict(myplsda, testDatos[,–14])
confuTest = table(testDatos$problema_corazon, mypred)
confusionMatrix(confuTest)
## Confusion Matrix and Statistics
## mypred Accuracy : 0.8448
## 0 1
## 0 28 3 Kappa : 0.6859
## 1 6 21 Balanced Accuracy : 0.8493
El modelo tiene unos valores similares (accuracy y kappa) para datos que nunca ha visto, con lo cual se puede concluir que este modelo, predice de forma bastante buena si un nuevo caso va a tener un problema de corazón o no con una probabilidad del aproximadamente 84% (Accuracy 0.84)
5.4 Discusión de los resultados
Se puede ver como el PLS-DA es un muy buen método para predecir nuevos casos de problemas de corazón en pacientes, sin embargo, cabe destacar que el estudio constaba de unos 300 pacientes aproximadamente por lo que habría que aumentar el número de individuos para observar si realmente este modelo PLS-DA predice con tanta seguridad (84%) si un paciente tendrá un problema del corazón o no. Por otro lado, se ha estudiado tanto la matriz de scores como la de loadings en dos componentes (las más significativas) y se ha estudiado las diferencias con los resultados del FAMD.
6. Conclusiones
6.1 Comparativa métodos utilizados
En este trabajo, se han utilizado tres métodos: FAMD, Clustering jerárquico y PLS-DA.
Tanto en el FAMD como en el clustering se han visto prácticamente los mismos resultados (información que se encuentra en el apartado de conclusiones del respectivo método) esto tiene sentido ya que se han utilizado las coordenadas de los individuos en las primeras seis componentes principales para realizar el clustering jerárquico, por tanto el FAMD nos ha servido como preprocesado de datos (para el clustering) y también como un primer análisis de las relaciones entre las variables y los individuos de nuestra base de datos. En el clústering hemos confirmado aquellas primeras observaciones que hacíamos sobre la existencia de dos grupos y las variables que influyen en los mismos. El PLS-DA, aunque también se ha utilizado para comparar los resultados con los del FAMD debido a la posible similitud entre los gráficos de Scores y de Loadings, se ha utilizado principalmente para evaluar la capacidad predictiva del modelo con nuestros datos. Descubriéndose así la gran capacidad predictiva del modelo con un accuracy del 85% en datos que nunca había visto (datos test).
6.2 Discusión sobre los métodos no aplicados
Los métodos que no se han usado en este trabajo son: Reglas de asociación, análisis discriminante.
En primer lugar, no se utilizan reglas de asociación porque consideramos que no se ajustaba a nuestra base de datos (nuestras variables no son cualitativas y el hecho de transformar todas las variables hubiera supuesto una pérdida importante de información). En cambio, el clustering y la posibilidad de realmente poder observar los clusters en los que se separaba nuestra base de datos nos parecía una opción mucho más interesante.
Con respecto al análisis discriminante, es cierto que hubiera sido una opción muy interesante ya que precisamente nuestra intención desde un primer momento es ver las variables que más relación tienen con el hecho de tener un problema de corazón o no, para luego predecir futuros casos o clasificar los individuos los cuales ya disponíamos. Sin embargo, el PLS o PLS-DA era obligatorio usarlo y ya se habían realizado los análisis de FAMD y clústering, los cuales se consideran más relevantes en este caso que el análisis discriminante, por lo tanto se ha decidido prescindir de él.
Por último, la elección entre PLS y PLS-DA es obvia ya que la intención siempre ha sido el estudiar la relación entre problema del corazón y el resto de variables por lo tanto la mejor opción en este caso es elegir PLS-DA, usando como Y problema del corazón y como X el resto de variables para estudiar la relación entre las mismas y la capacidad de predicción.
7 Otros temas
7.1 Comentarios sobre artículos leídos
La idea de sacar tanto el FAMD como el clustering jerárquico (así como el hecho de usar la matriz de scores para el clustering jerárquico) ha surgido del libro ‘Practical Guide To Principal Component Methods in R (Kassambara)’ y del libro ‘Exploratory Multivariate Analysis by Example Using R (Chapman & Hall/CRC Computer Science & Data Analysis)’ de Francois Husson. Creemos que se trata de una herramienta muy poderosa el hecho de combinar ambas técnicas (FAMD y clústering) ya que primero, nos permite quitar ruido de nuestros datos, y segundo, usando como preprocesado el FAMD podemos usar ‘mixed data’ en clústering, lo cual nos aporta un gran beneficio.
8. Ánexo:
8.1 Blibliografía
- HCPC I
- FAMD I
- Pendiente Segmento ST información
- ‘Practical Guide To Principal Component Methods in R (Kassambara)’
- ‘Exploratory Multivariate Analysis by Example Using R (Chapman & Hall/CRC Computer Science & Data Analysis)’ de Francois Husson
- Documentación FactoMineR
- Cambios en el corazón y los vasos sanguíneos por el envejecimiento
- Latidos por minuto máximos
- Factores de riesgo problemas cardiovasculares
- Datos utilizados
8.2 Análisis distribución de las variables
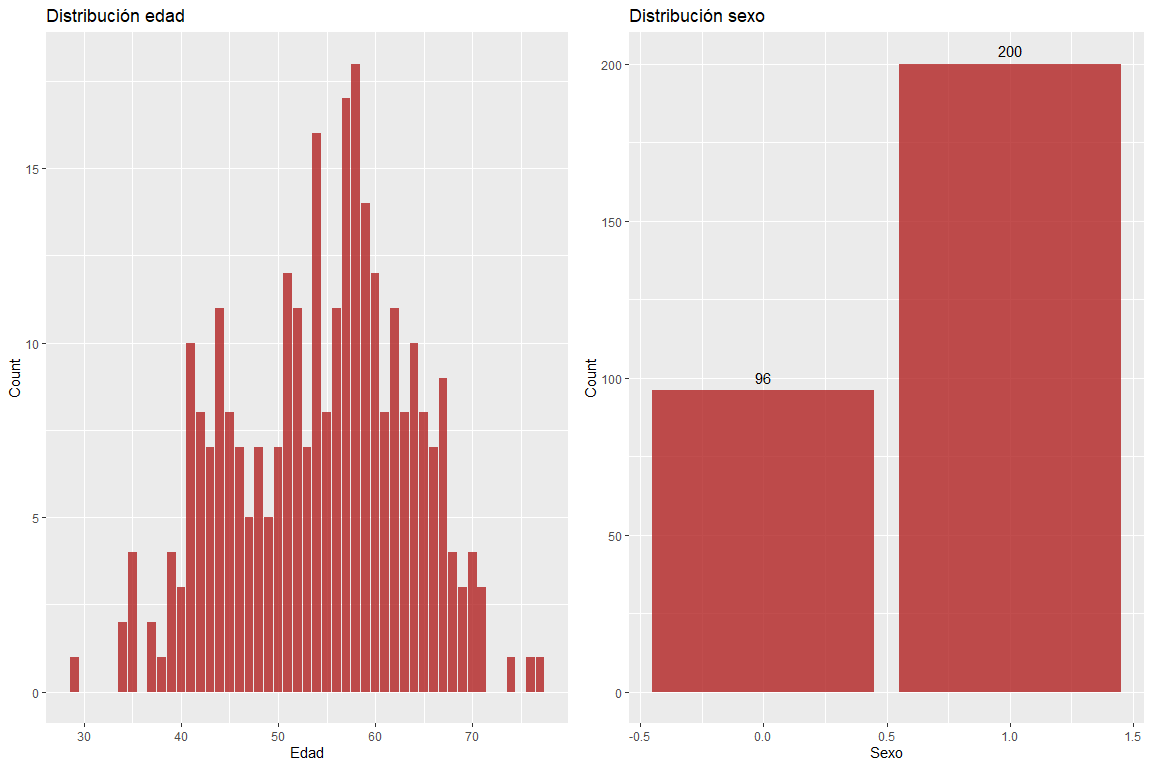
La variable edad no toma valores extremos y la variable sexo no contiene valores erróneos.
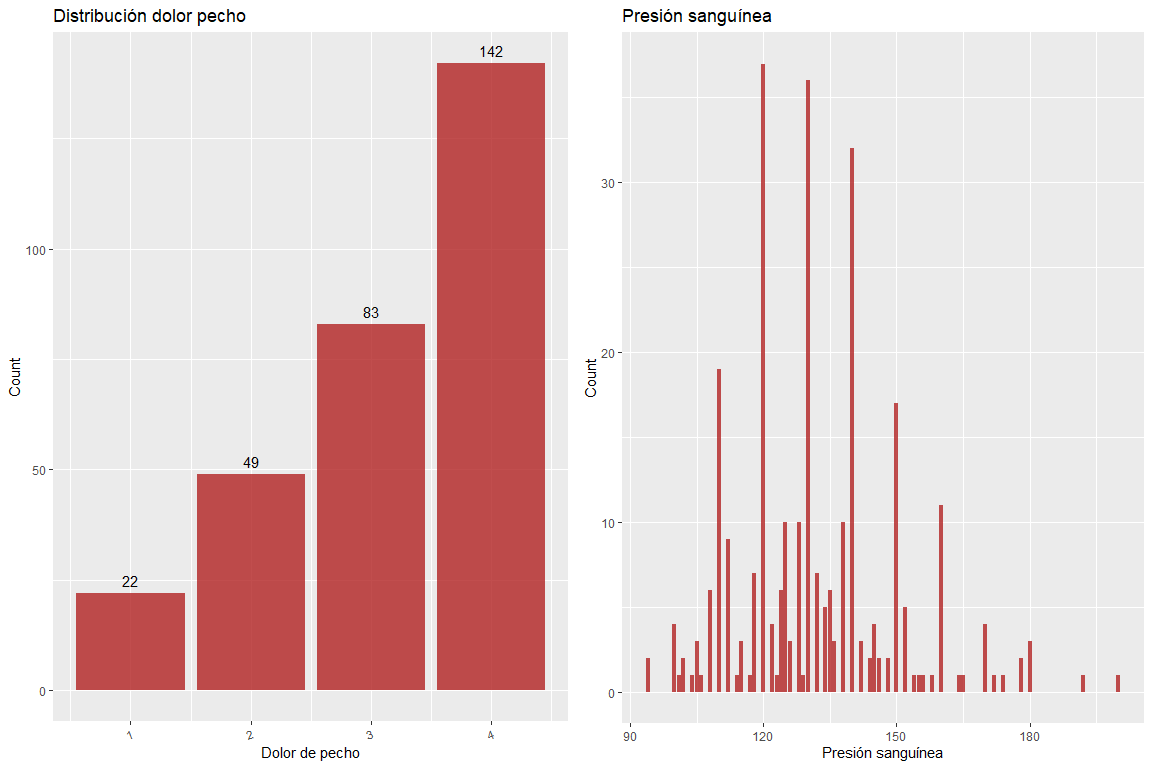
La variable dolor de pecho no contiene valores erróneos, así como tampoco lo hace la variable presión sanguínea.
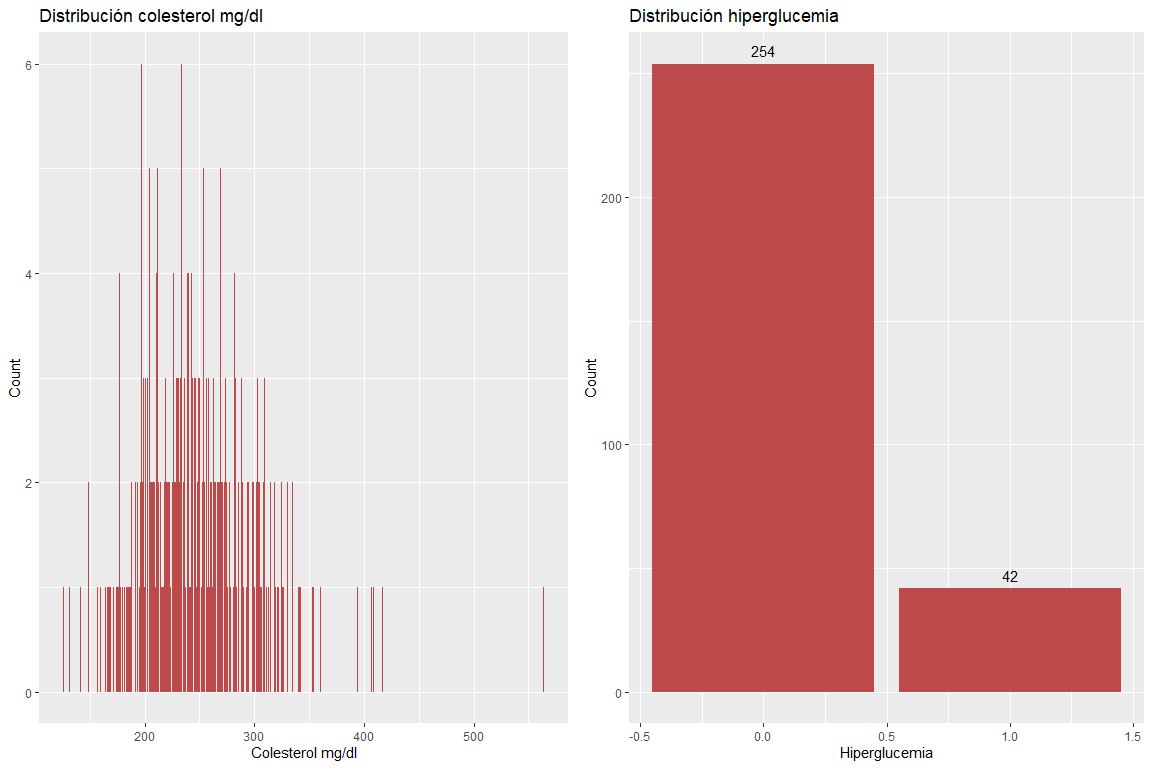
Las dos variables Colesterol mg/dl e hiperglucemia no toman valores erróneos.
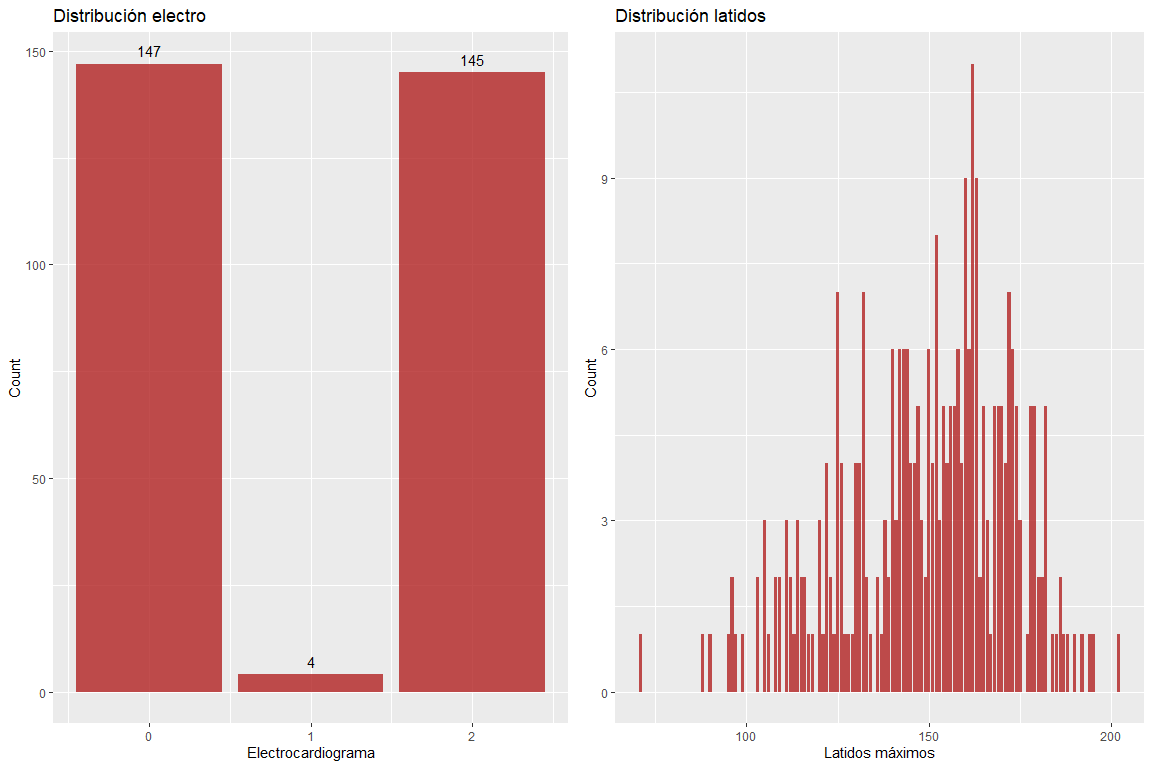
Las dos variables resultados del electrocardiograma y latidos máximos por minuto no toman valores erróneos. Sin embargo hay que recalcar que hay valores un poco elevados para la edad de los pacientes (según la fórmula de Haskell & Fox, cuyo uso está muy extendido para delimitar las pulsaciones máximas según la edad).
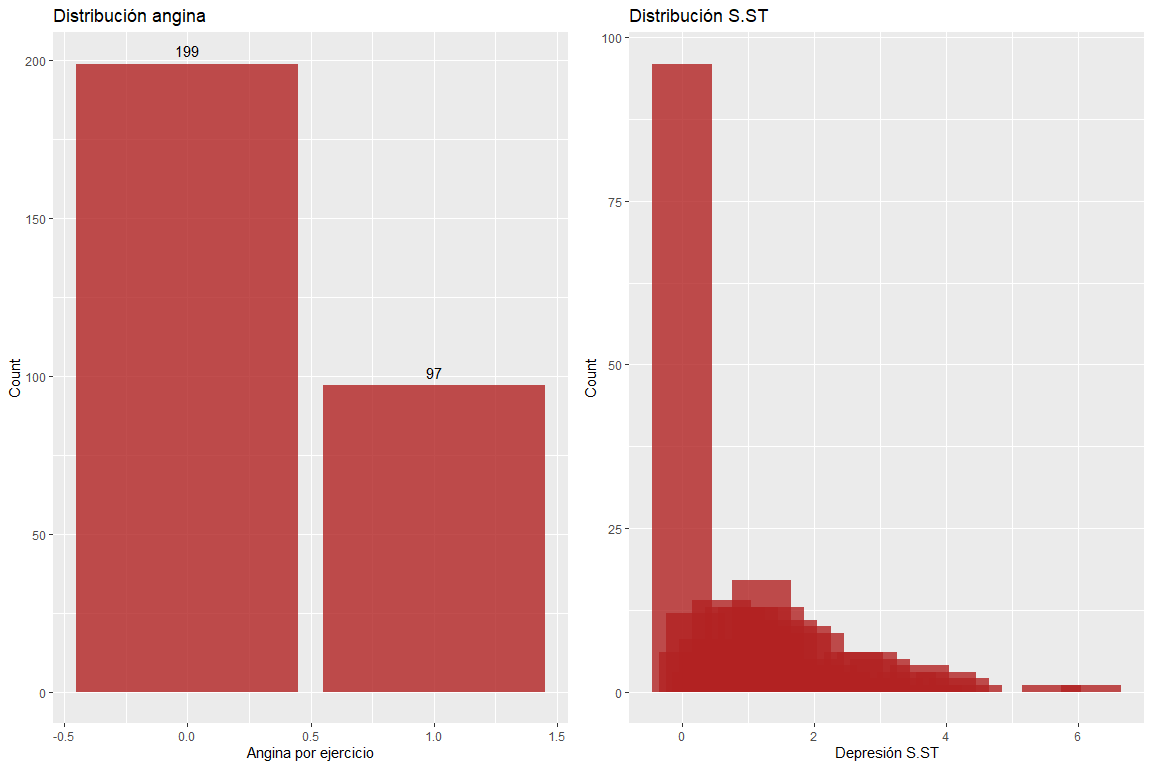
Las dos variables angina por ejercicio y depresión del segmento ST no tienen valores erróneos. Pero hay que recalcar que hay observaciones con un valor de depresión del segmento ST muy alto.
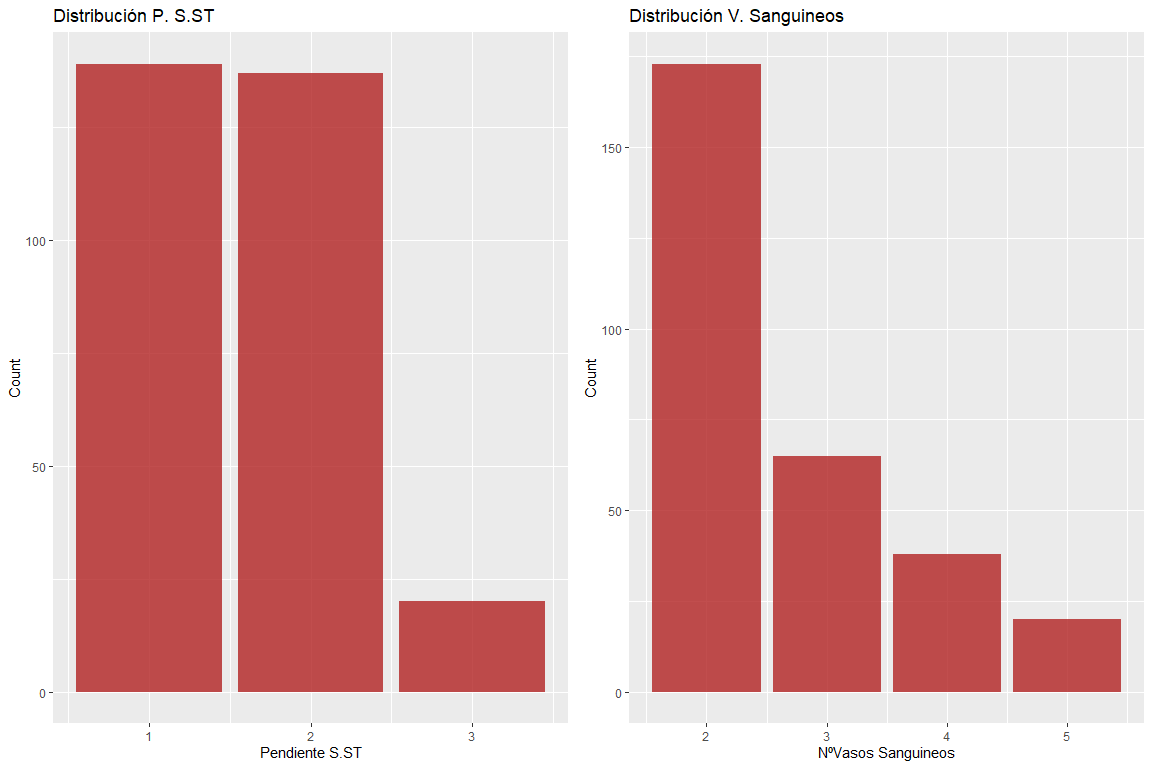
Las dos variables pendiente del segmento ST y nº de vasos sanguíneos no tienen valores erróneos.
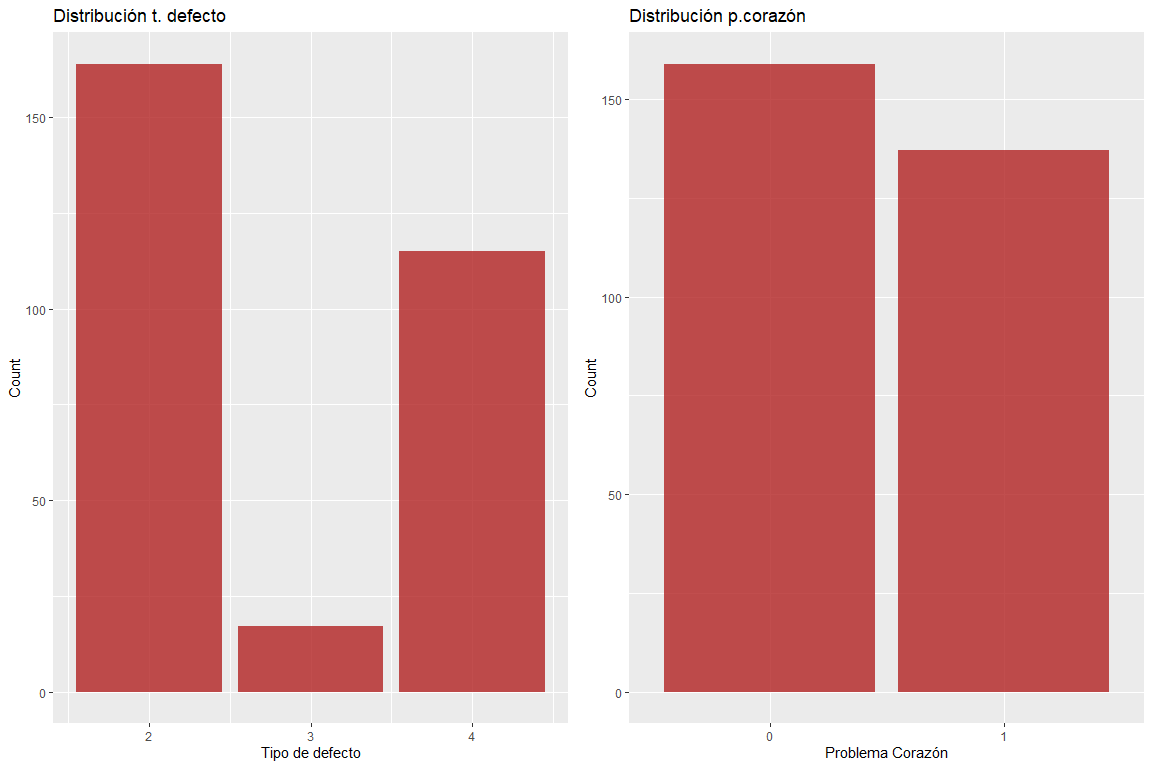
Las dos variables tipo de defecto y problema de corazón no tienen valores erróneos.